Syntax
Here, term syntax basically refers to everything that does not have to do with the values bound to variables in the initial environments. Most importantly, the library functions (or preamble, or standard procedures, et c) are not included here.
It might be confusing, though, to find that many of the composite expression syntaxes are implemented as function calls, which the user may become aware of when encoutering certain error messages.
Lexer directives are parts of the program that give special instructions to the Shapes compiler, rather than being passed to the parser to become part of the abstract syntax tree. All lexer directives begin with ##, and must be the first thing on a line except for leading whitespace. This section presents both lexer directives for file inclusion, lexer directives that don't fit in any other section, and the syntax for source code comments.
Other lexer directives include those related to
LaTeX and those related to
namespaces.
Files are included using the lexer directives
##needs and
##include. The
##needs directive is used to require extension sources to be loaded, and will only load each source once in any namespace. This avoids the duplicate definitions that would occur if the source was loaded several times in the same namespace. It is strongly recommended not to use
##needs but in the global namespace, unless doing so leads to identifier collisions (identifier collisions and namespaces in general are discussed in detail
below. The
##include directive will load the source unconditionally, and is used with application sources.
The syntax is for unconditional inclusion of an application source file is
##include filenamebase (: _ directory)?
(Note the mandatory whitespace after the colon). Examples:
##include background
##include foreground : ~/Library/Shapes/Project Templates
The loaded file must have the
.shape suffix, which must not be present in the
##include directive. There is currently no support for including blank mode sources, although it may be added in the future.
Note that the whitespace before directory is eaten up, while the whitespace in the directory name is kept.
The interpreation of the
filenamebase is with respect to the
need search path, see the
man page.
The syntax for ensuring that a Shapes extension source has been loaded is
##needs filenamebase.shext (: _ directory)?
##needs namespace (: _ directory)?
##needs namespace / filenamebase (: _ directory)?
Here, the optional
directory has the same meaning as with
##include. The first form is called the
filename form of ##needs, and the other two constitute the
namespace form of ##needs. The only difference between the filename form of
##needs and
##include is that they work with different filename suffixes and that
##needs will not load the file if it is already loaded.
Examples of the namespace form:
##needs Blockdraw
##needs ..A..B : ~/Documents/ShapesExtras
##needs Foo..Bar / stuff
##needs / helpers
##needs .. / book_settings : ~/Library/Shapes/Project Settings
Any relative namespace, like Shapes..Blockdraw above, is first interpreted relative to the current namespace, so that the operation is always described in terms of an absolute namespace. This absolute namespace is mapped to a file location in a directory hierarchy, with each namespace level corresponding to a file system directory. For a directory to be considered part of the directory hierarchy, it must contain a file named Shapes-Namespace.txt, which is a declarative specification of the contents of the associated namespace.
In the form without filenamebase, the entire content of the namespace will be loaded, as described by the Shapes-Namespace.txt in the namespace directory, including all subdirectories that are part of the namespace directory hierarchy.
In the form with filenamebase, only filenamebase.shext will be loaded from the namespace directory.
It is not allowed to use a relative namespace beween ##push ^^ and ##pop ^^, since the encapsulation namespace does not have a name that can be mapped to a directory in the file system.
A
Shapes-Namespace.txt may contain comments and a small number of declarative pieces of information. Each directive begins at the beginning of a line, and directives that take arguments may be written over multiple lines by using leading spaces on subsequent lines:
# This is a comment.
encapsulated # Encapsulate namespace content.
prelude: basic.shext # prelude: is a directive that takes a list of files and directories.
"things.shext" # Filename delimited by quotation marks.
Sub1 Sub2 # Multiple items on the same line.
order: this.shext < that.shext < last.shext # Load this.shext before that.shext, and that.shext before last.shext.
order:
first.shext
<
Sub1 Sub2 Sub3
<
last.shext
ignore:
tmp.shext
foo.shext
doc
Files that don't have the
.shext suffix and directories not containing a
Shapes-Namespace.txt file are automatically ignored. The order of the arguments only matters for the
order: directive; the
prelude: directive just specifies a subset where the items will be visited in the same order as if the entire namespace would be loaded. Normally, neither the
order: nor the
ignore: directive should be needed.
The encapsulated directive tells ##needs to wrap the content of the namespace in an encapsulation namespace. This encapsulation namespace will be the same encapsulation namespace each time ##needs loads a file in this part of the directory hierarchy. (This is in contrast to ##push ^^, which always creates a new encapsulation namespace.)
Multi-line comments are delimited by /** and **/, and nest. It is recommended that multi-line comments begin each line with **. It is also recommended that no code is put on the same line as a multi-line comment, since it will be very hard for the eye to see what really is commented out.
Rest-of-line comments start with |**.
The designers of the c++ language may have a good point when they say that rest-of-line (also known as single line, or c++ style) comments is the only type of comment to be used to comment out code. Whether they think that rest-of-line comments may also be used for comments I don't know, but I think it would be a good idea to reserve the use of rest-of-line comments for only commenting out code, and to use multiline comments for comments (documentation).
The following directive allows a source file to print a message to
stdout when the file is scanned:
##echo text-to-end-of-line-will-be-echoed
You can put your name in the
pdf file using the following directive:
##author your name
It can be used both in application files and in extension files, although it is not treated as the main author of the produced document in the latter case.
The srand function in the Standard C Library, can be accessed through
##seed integer
although I don't think there is any reason to do so. Please consult the documentation on the random number facilities for an explanation.
Shapes uses a
namespace concept similar to that found in
c++ and many other languages. Most importantly, namespaces allow Shapes extensions to introduce bindings in the global scope without polluting the global namespace. In fact, Shapes itself only introduces bindings in the
Shapes namespace, so that the global namespace is empty at the beginning of every program (except for misbehaving preamble code added by the user).
Before introducing the namespace-related lexer directives, we need syntax definitions for namespaces:
Similar to Java, the namespace of a Shapes extension is hard-coded. One could say that there is no such thing as changing the namespace of an extension; you can stop maintaining the extension in its original namespace and make a clone of it in another namespace, but the users of your extension will need to go through a more or less painful process to migrate from the old extension in the old namespace to the new extension in the new namespace. Using an extension as if it were placed in a different namespace than where it is defined is not possible (since the complexity that such design brings outweighs the benefits).
For a single user, hard-coded namespaces is probably not a big issue, but the situation gets more complicated when individuals and organizations start sharing code with each other. The risk of conflicting use of namespaces is obvious, and the solution is to define who is in charge of allocating namespaces in various subtrees of the entire namespace tree:
-
.. is under the control of this very section in the documentation.
-
..Shapes is managed by the Shapes project and reserved for the core bindings and standard extensions of the Shapes language.
-
..net is an example of a reverse DNS top level namespace; all lowercase-only top level namespaces are reserved for implicit reverse DNS mapping.
For example
..net..sourceforge belongs to
SourceForge. This means that SourceForge
may decide that each project gets to manage its own namespace, either immediately under
..net..sourceforge, or at some deeper level such as
..net..sourceforge..proj. Note that not all valid domain names have a corresponding namespace, only domain names where each part is a valid
identifier have a corresponding namespace.
-
..User is reserved for implicit mapping of
email addresses to namespaces. Not all valid email addresses have a corresponding namespace, but only those where each part of the host name, and the entire local part is a valid
identifier. The mapping is then defined by first doing reverse DNS mapping of the host name, and then append the local part. For example,
..User..net..sourceforge..tiddishsource is managed by the owner of the
tiddishsource user account at SourceForce.
Normalization of the local part may be applied to yield a valid namespace identifier. For example, a user with email address foo.bar@gmail.com is the manager of ..User..com..gmail..foobar, since gmail.com treats foobar and foo.bar the same. Note that different email hosts may apply different normalizations.
-
..Alias is managed by the Shapes project and reserved for namespaces explicitly allocated to users of Shapes. Each namespace directly under ..Alias is managed by some user, and provide a more compact alternative to the implicitly allocated namespaces under ..User. Each user must provide a valid link for getting in touch, such as an email address, a Facebook account, a SourceForge profile, etc.
The following namespaces are currently allocated:
| Namespace | Belongs to |
..Alias..tidde | |
-
..Applications is managed by the Shapes project and reserved for generally useful applications that demonstrate the use of the Shapes language, and that are distributed together with Shapes.
-
..Contrib is managed by the Shapes project and reserved for user-contributed extensions of general interest that are distributed with Shapes. Namespaces allocated directly under ..Contrib shall be listed here, but at the moment there are none.
Let us begin by briefly mentioning the different lexer directives that relate to namespaces. To add a namespace to the list of places where to look for identifiers, use
##lookin Some..Namespace
To append a namespace identifier to the end of the current namespace, do (
more variants will be presented below)
##push MyPackage
and then, once you are done and need to restore the current namespace, do
##pop MyPackage
where the namespace identifiers are required to match for the sake of redundancy and readability.
To introduce
alternative an alias for the namespace
original, do
##alias alternative = original
Three different kinds of bindings can be inserted into a namespace:
##push A
x: 1 /** Introduces a binding for a variable in namespace A **/
•y: newGroup /** Introduces a binding for a state in namespace A **/
dynamic @z identity 1 /** Introduces a binding for a dynamic variable in namespace A **/
##end A
They ways in which bindings can be introduced is discussed in detail in
Code bracket. In this section, we will look at how the bindings are referred to.
The different kinds of references are recognized by looking at the prefix of the identifier. For example, a lexical variable uses no special prefix, and may look like stroke or Shapes..Graphics..stroke. A dynamic variable uses the prefix @, and may look like @spot or Shapes..Graphics..@spot. A state is prefixed with • or #, like •page, Shapes..IO..•page, or #dst. For the current discussion of namespaces, we will use lexical variables in our examples, but the rules are the same for any kind of reference or binding.
A lexical variable reference consists of an optional namespace qualifier and an identifier. The namespace qualifier may be either absolute, local, or relative, and contains a sequence of zero or more namespace identifiers. The length of a namespace qualifier is its number of namespace identifiers. The written representation of a namespace qualifier uses the namespace separator to separate the namespace identifiers, and has a leading namespace separator in case it is absolute, or a leading ^^ in case it is local. There is no way to visually distinguish between an identifier of a lexical binding and a namespace qualifier, so the intention needs to be clear from the context. For example, in the context of namespace paths, Shapes and MyPackage..Impl are relative namespace paths, ^^MySubPackage and ^^ are local namespace paths, while ..Shapes and .. are absolute namespace paths. The special case of a relative namespace path without any namespace identifier has an empty written representation. The namespace path .. is called the global namespace.
References are similarly divided into absolute, local, and relative based on their namespace qualifier. References without namespace qualifier are relative. The written representation of a reference begins with its namespace qualifier and ends with the simple identifier. Only if the namespace path contains at least one namespace identifier are the two separated by a namespace separator. For example ..Shapes..stroke (with separator) and ..background (without separator) are absolute identifiers, while Shapes..stroke (with separator) and stroke (without separator) are relative identifiers.
The nomenclature introduced above is formalized syntactically with the following definitions.
For example, the lexical structure covers the following cases for a
lex-var:
x /** Relative reference with empty namespace path **/
^^x /** Local reference with empty namespace path **/
..x /** Absolute reference with empty namespace path **/
A..x /** Relative reference with non-empty namespace path **/
^^A..x /** Local reference with non-empty namespace path **/
..A..x /** Absolute reference with non-empty namespace path **/
From the lexer's myopic point of view (that is, by just looking at the characters which consistute the identifier), a simple identifier by itself is a relative identifier which happens not to contain any namespace identifiers. However, from the parser's point of view, a simple identifier may play two quite different roles. When bindings are introduced, this is always done using simple identifiers, and — for reasons that will become clear later — then the simple identifier is also denoted a placed identifier.
Namespace aliases may be introduced to reduce the amount of typing needed and to increase maintainability of the code (by reducing the amount of duplicated namespace paths appearing in identifiers). Aliases are introduced using the
namespace-alias lexer directive. When defining an alias like
##alias A = B..C
the alias
A is installed in the current namespace of the lexical environment, so it is like a placed identifier but for a namespace. The expansion of the alias
B..C is resolved relative to the namespace where the alias is defined.
The intention of namespace aliases is to use them as an implementation facility, not to provide alternatives in code interfaces. To this end, a namespace alias will only be matched against the first namespace identifier of a relative namespace path. It still means that if the same namespace is opened up in different places (possibly even in different source files), an alias introduced in one place will be visible in the other. This is considered a minor deficiency of the design, see the note below. The following example shows this and some other aspects of namespace aliases. The exact details of
Lookup rules will be given below.
| Namespace aliases |
|---|
|
Defining and using namespace aliases.
|
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
/** Populate a namespace hierarchy.
**/
##push W
##push X
##push Y
##push Z
a: 1
##pop Z
##pop Y
##pop X
##pop W
/** Alias with absolute expansion, placed in the global namespace
**/
##alias K = ..W..X..Y
/** The alias can be accessed using a relative identifier.
**/
{
res: [Debug..locate (resolved_identifier_string K..Z..a)]
IO..•stdout << `Resolving ´ << [Debug..sourceof res] << ` within ´ << (resolved_identifier_string @@) << `: ´ << res << "{n}
}
##push W
/** Alias with relative expansion
** The expansion is resolved relative to the current namespace (here ..W)
**/
##alias L = X..Y
/** Expand the alias from a nested namespace.
**/
##push R
{
res: [Debug..locate (resolved_identifier_string L..Z..a)]
IO..•stdout << `Resolving ´ << [Debug..sourceof res] << ` within ´ << (resolved_identifier_string @@) << `: ´ << res << "{n}
}
##pop R
##pop W
##push W
/** Expand the alias from the same namespace opened again.
**/
{
res: [Debug..locate (resolved_identifier_string L..Z..a)]
IO..•stdout << `Resolving ´ << [Debug..sourceof res] << ` within ´ << (resolved_identifier_string @@) << `: ´ << res << "{n}
}
##pop W
/** Namespace aliases are only followed for the first namespace name in a namespace path.
** This is to allow an extension to use aliases for its own convenience, without the risk that
** users of the extension create dependencies to these aliases.
**
** This wouldn't work:
**/
|**{
|** res: [Debug..locate (resolved_identifier_string W..L..Z..a)]
|** IO..•stdout << `Resolving ´ << [Debug..sourceof res] << ` within ´ << (resolved_identifier_string @@) << `: ´ << res << "{n}
|**}
|
|
| stdout:
show/hide
|
Resolving K..Z..a within ..: ..W..X..Y..Z..a
Resolving L..Z..a within ..W..R..: ..W..X..Y..Z..a
Resolving L..Z..a within ..W..: ..W..X..Y..Z..a
|
|
A different namespace alias design has also been prototyped, but remains undocumented in favor of the aliases explained above. In the other design, the aliases are not installed as links in the namespace hierarchy. Instead they are only visible in the lexical surrounding where they are introduced. These namespaces can be used to do more things and not storing the aliases in the namespace hierarchies is arguably cleaner, but they also make identifier lookup considerably more complicated. The current design was chosen because of its simplicity that makes identifier lookup transparent and with less risk of unexpected lookup hits.
|
At the point where evaluation of a Shapes program begins, the current namespace is the global namespace. It is then changed using
##push,
##pop, and
##needs. The first two have already been mentioned, always come in pairs, and have to obey certain rules:
- A ##pop must match the most recent, not already matched, ##push completely.
- A ##push must have its matching ##pop in the same code bracket.
- A ##push must have its matching ##pop in the same file.
Three different types of namespaces can be used with
##push and
##pop:
- Named namespace
- Private namespace
- Encapsulation namespace
each of which is described below.
The remaining way of controlling the current namespace is using the
namespace form of ##needs. The file being loaded by this lexer directive will be loaded in the absolute namespace of the directive (recall that if a relative namespace is given, it is interpreted relative to the current namespace to yield an absolute namepsace).
The most elementary form of
##push (shown above) deals with named namespaces, and is a special case of
##push RelativeNamespacePath
which appends the given relative namespace path to the current namespace. Example:
/** Current namespace is the global namespace. **/
##push MyPackage
/** Current namespace is MyPackage **/
##push A..B
/** Current namespace is MyPackage..A..B **/
##pop A..B
/** Current namespace is MyPackage **/
##pop MyPackage
/** Current namespace is the global namespace **/
Each time a non-private namespace is pushed, a unique private namespace is set up for keeping implementation details away from the public part of the namespace. The
private namespace is represented by a single dash:
##push -
and can be opened and closed multiple times, just like a named namespace. Unlike a named namespace, there is no way to refer to a private namespace using a namespace path. Special
lookup rules apply in the namespace containing the private namespace, to provide a way of accessing the implementation in a controlled way.
When the current namespace is not private, it is called normal.
| Private namespaces |
|---|
|
Principles of private namespaces.
|
|
| Source:
show/hide
—
visit
|
/** This example demonstrates private namespaces.
**/
/** Pushing a named namespace sets up a new unique private namespace: **/
##push A
/** Open the private namespace a first time: **/
##push -
x: 1 /** Implementation detail of A. **/
/** Source code reflection of the private namespace shows a namespace identifier in
** the form of a unique number:
**/
Shapes..IO..•stdout << `Current namespace: ´ << (resolved_identifier_string @@) << "{n}
##pop -
/** Access implementation detail from the private namespace using relative identifier
** with empty namespace path:
**/
Shapes..IO..•stdout << (resolved_identifier_string x) << "{n}
/** Open the private namespace a second time: **/
##push -
Shapes..IO..•stdout << `Current namespace: ´ << (resolved_identifier_string @@) << "{n}
/** The private variable x is still in scope here. **/
Shapes..IO..•stdout << (resolved_identifier_string x) << "{n}
/** Implement some functions in the private namespace. **/
foo: \ y → x + y
bar: \ y → x - y
baz: \ y → x * y
##pop -
/** Expose the functions foo and bar from the private namespace by
** providing bindings in the normal namespace:
**/
": foo /** Refers to binding in private namespace; this is not a circular refrence. **/
b: bar /** Expose bar under a different name. **/
baz: - /** Special syntax for exposing private namespace variable of the same name. **/
/** Verify that the private namespace has precedence over the normal namespace: **/
Shapes..IO..•stdout << (resolved_identifier_string foo) << "{n}
##pop A
/** One cannot access the private binding here; something like A..x won't work. **/
/** Pushing the same named namespace again sets up a new unique private namespace: **/
##push A
##push -
Shapes..IO..•stdout << `Current namespace: ´ << (resolved_identifier_string @@) << "{n}
/** The variable x is not in scope here, since this is a different private namespace. **/
/** The foo in the other private namespace is no longer in scope: **/
Shapes..IO..•stdout << (resolved_identifier_string foo) << "{n}
##pop -
/** Neither is x in scope here. **/
##pop A
/** The exposed bindings can still be accessed in the normal namespace: **/
Shapes..IO..•stdout << (resolved_identifier_string A..baz) << "{n}
|
|
| stdout:
show/hide
|
Current namespace: ..A..8..
..A..8..x
Current namespace: ..A..8..
..A..8..x
..A..8..foo
Current namespace: ..A..9..
..A..foo
..A..baz
|
Namespaces in Shapes serve two different purposes at the same time:
- Organization of more or less related (often unrelated) Shapes extensions by associating an extension with its own namespace.
- Organization of code within a piece of code that belongs together.
Each purpose taken by itself is served very well by the namespace mechanism, but when in use for the two purposes at the same time there is a risk that one is mistaken for the other, a potential source of serious maintainability issues.
An
encapsulation namespace is a way of restricting the lookup of relative identifiers (detailed
lookup rules will be given below). It is used allow namespaces to safely serve their two purposes at the same time.
There are two mechanisms for introducing encapsulation namespaces, one using
##push, and one using the
namespace form of ##needs. With
##push, an encapsulation namespace is represented by a sequence of two circumflexes:
##push ^^
In this form, a new encapsulation namespace is created each time. With
##needs, the same encapsulation namespace may be entered multiple times
When a binding or namespace is created in the encapsulation namespace, an entry with the same name is also added in the surrounding namespace. This means that two encapsulation namespaces under the same named namespace cannot introduce the same bindings or contained namespaces.
There is always a current encapsulation namespace, referring to the closest surrounding encapsulation namespace, defaulting to the global namespace. By construction, the current encapsulation namespace will always be a prefix of the current namespace. In addition to restricting lookup of relative identifiers, an encapsulation namespace also serves as a base for local identifiers.
| Encapsulation namespaces |
|---|
Principles of encapsulation namespaces, illustrated with ##push ^^ and ##pop ^^. Encapsulation namespaces may also be introduced by the namespace form of ##needs. |
|
| Source:
show/hide
—
visit
|
/** This example demonstrates encapsulation namespaces.
**/
##push A
w: 4
/** Open an encapsulation namespace: **/
##push ^^
/** The variable w is not in scope here. **/
/** Introduce a binding in the encapsulated namespace (also creating a binding in A): **/
x: 1
/** Open a namespace inside the encapsulation namespace: **/
##push B
y: 2
x: 3 /** Shadowing binding. **/
/** Use a local reference to refer to the shadowed binding: **/
Shapes..IO..•stdout << ^^x << "{n}
##pop B
##pop ^^
/** Open another encapsulation namespace: **/
##push ^^
/** The variable x is not in scope here, since this is a different encapsulation namespace.
** However, it would cause a conflict if x was introduced here as well, as there is already
** a binding for x in A.
**
** Similarly, it is not possible to open a namespace called B here.
**/
##pop ^^
##pop A
/** The encapsulation namespace isn't seen from the outside: **/
Shapes..IO..•stdout << (resolved_identifier_string A..x) << "{n}
Shapes..IO..•stdout << (resolved_identifier_string A..B..y) << "{n}
z: A..x + A..B..y
|
|
| stdout:
show/hide
|
1
..A..x
..A..B..y
|
Setting up
look-in namespaces is an alternative to namespace aliases, as an approach to reducing the amount of typing and increasing code maintainability. Look-in namespaces are added using the
namespace-lookin lexer directive. When adding a look-in namespace like
##lookin A..B
the namespace
A..B will be searched as a last resort for relative identifiers. For example,
##push A
x: 1
##push B
y: 2
##pop B
##pop A
##lookin A
x + B..y
is a valid way of adding
A..x and
A..B..y.
The look-in namespace is resolved relative to the namespace where the look-in is set up, allowing for all types of namespace references:
##lookin A..B |** Relative namespace path
##lookin ^^A..B |** Local namespace path
##lookin ..A..B |** Absolute namespace path
When a relative namespace path is resolved, it is simply appended to the current namespace, without searching surrounding namespaces for a match. If the referenced namespace turns out to be empty, the look-in is still valid, only useless.
When a reference is looked up, several look-in namespaces may be in scope. The look-in namespaces will be tried in order from most to least recently added, and the search is terminated as soon as the reference is resolved. This means that adding a look-in namespace may shadow bindings in existing look-in namespaces. The list of all look-in namespaces in scope, in the order in which they will be tried, is called the
look-in sequence. See
Lookup rules for additional details.
While look-in namespaces and namespace aliases address the same need, the following look-in namespace details are not shared by namespace aliases:
- A look-in namespace is only in scope until the current namespace is popped (recall that a namespace alias is still visible if the same namespace is pushed again).
- A look-in namespace is not propagated to other files loaded with ##needs.
- A look-in namespace is not bound to the current environment.
- There is no sign of a look-in namespace where it is used (compare a namespace alias, which is present in the first namespace identifier).
Considering these differences, some recommendations can be formulated regarding when to use a namespace alias and when to use a namespace look-in:
- Consider defining a namespace alias the primary option for the sake of readability. For one thing, the less complicated semantics of aliases makes code more intuitive. Second, the fact that the alias name is present where it is used makes code more explicit.
- Avoid relying on a namespace alias in a place where its definition cannot be readily found.
- Only use a look-in namespace when the namespace content can be considered well known, so that a reader of your code can easily figure out which references rely on the look-in namespace. For example, it could be considered well known that the stdout stream is accessed via ..Shapes..•stdout, so adding a look-in for Shapes and then just using the reference •stdout would be fine.
- Use a look-in namespace when you don't want to litter the current namespace with an alias. This would only be a concern when the current namespace is expected to be pushed again somewhere where the alias definition is not readily seen.
- Use a look-in when an alias wouldn't do the job since the bindings of interest reside outside the current environment.
During program evaluation, every expression has a lexical environment. Each environment has a set of mappings from absolute identifiers to values (bindings). Except for the global environment, each environment also has a parent environment. Although bindings are only present during program evaluation, the identifiers being bound are static, allowing identifiers to be looked up during static analysis.
At every point in a program, there is also a
search context which defines how an identifier appearing at that point will be looked up. The search context consists of four parts:
- The current namespace.
- The current encapsulation namespace.
- The private namespace (not always defined).
- The look-in sequence.
Each of these has been introduced in earlier sections, and now it is time to go into the details of how they they are used during look-up.
When a binding is introduced, a simple identifier is placed in the current namespace. No look-up is involved; a binding can never be introduced anywhere but in the current namespace (although mechanisms exist which may give the impression that a binding is introduced in the parent namespace). This is why a placed (in contrast to looked up) identifier is always a simple identifier.
Lookup of references will be explained in the following order:
- Absolute, like ..A..B..x (or just ..y if the namespace path happens to be empty).
- Local, like ^^A..B..x (or just ^^y if the namespace path happens to be empty).
- Relative, like A..B..x (or just x if the namespace path happens to be empty).
An absolute reference (like
..A..B..C..x) is looked up as follows (recall that a namespace alias may only be matched against the first namespace identifier of a relative reference):
- Start with the lexical environment.
- Search for an exact match of the entire reference in the environment, ignoring namespace aliases.
- If found, this is the result of the elementary look-up.
- If not found, and the environment is the global one, the elementary look-up is a failure.
- Otherwise proceed with the parent environment.
Note that an absolute reference can never refer to a binding in a private namespace, or make use of look-ins or aliases. However, an absolute reference can refer to the contents of an encapsulation namespace via the links into the encapsulation namespace.
A local reference (like
^^A..B..C..x) is looked up as follows:
- Construct an absolute reference by prepending the current encapsulation namespace to the local reference.
- Look up the absolute reference.
Just like an absolute reference, a relative reference can never refer to a binding in a private namespace, or make use of look-ins or aliases. If there are nested encapsulation namespaces, only the innermost is accessible using local references.
A relative reference (like
A..B..C..x) is looked up as follows:
- Start with the lexical environment.
- Do look up in the environment at hand according to the rules below.
- If a match is found, this is the result of the elementary look-up.
- If not found, and the environment is the global one, the elementary look-up is a failure.
- Otherwise proceed with the parent environment.
A relative reference,
r, is looked up in a given environment by selecting the first rule below with a match:
- If the current namespace is normal and the reference has empty namespace path (the reference is just a simple identifier, like x), look up the reference in the private namespace.
- Search for the longest prefix p of the current namespace such that:
- The encapsulation namespace is a prefix of p.
- Prepending p to r yields a match for the resulting absolute reference, allowing namespace aliases to be followed for the first namespace identifier of r.
- Search the look-in sequence for a namespace which can be prepended to the relative identifier, yielding a match for the resulting absolute reference.
Note that look-up of a relative identifier is a search in two dimensions: the chain of linked environments (outer loop), and the length of the namespace prefix and the look-in sequence (inner loop).
When exposing selected content of a private namespace via bindings in the surrounding normal namespace, the basic mechanism for doing so is just an ordinary binding, often relying on the fact that the private namespace has priority over the current namespace:
main: main /** Refers to main in private namespace. **/
When this mechanism is used to clearly define a public interface, separate from the implementation, it has the disadvantage that the description of the public interface is cluttered with variables from the private namespace, and there is typically a lot of repeated identifiers. To support clean presentation of public interfaces, Shapes has a special form for bindings that are just alias for variables with the same name in the private namespace:
main: - /** Implemented in private namespace **/
The lookup rules differ from the explicit variant, in that the alias is only looked up in the private namespace. This both makes the intent of the new binding clear, and avoids the risk of confusion caused by cyclic references. In case the public interface wants to expose a private binding under a different name, the basic mechanism has to be used instead — there is no way to restrict lookup to only consider the private namespace in general.
One reason for not providing restriction to lookup in the private namespace in general is that this would require a somewhat heavier syntax than the current design. For example, one alternative would have been to allow
main: -.." /** Refer to 'main' in private namespace. **/
foo: -..bar /** Refer to 'bar' in private namespace. **/
However, since the pure alias form is expected to be much more common than the rename form, one has to prioritize syntax burden for this case, and then -.." cannot compete with the simplicity of a single minus. |
In this section we call a Shapes extension a module if it follows a pattern that clearly separates public interface from implementation, and that makes the public interface easy to read. Note that this is only one of many possible patterns to fulfill the same goal, and the term module has (as of today) no particular meaning outside this section. While the module pattern presented here places both public interface and implementation in the same file, it would also be interesting to consider how to define modules where the public interface has its own file, and the implementation may be spread over several files…
The main ideas are:
- Follow a simple template that will make it easy to read the file for anyone that is familiar with the template.
- Use standardized comments such as /** === End of public interface === **/ to clearly show the sectioning of the file.
- Place implementation in a private namespace at the end of the file.
- Define the public interface at the top of the file.
- The public interface is defined by exposing selected parts of the implementation in the private namespace.
- The names in the public interface do not necessarily have to be the same as those in the private namespace, but using the same name will avoid some clutter in the presentation of the public interface.
- The public interface shall be documented where it is defined — do the right thing and document each of the exposed bindings!
- Don't mess with the module's public namespace; users will expect to find the bindings in the namespace given by the namespace directory hierarchy.
- Optionally use namespace encapsulation to make the module more self-contained. If encapsulated, the module will be easy to move to another namespace later.
- If Shapes is equipped with an optional type system one day, it would also be a good idea to add type annotations to the exposed bindings.
A tiny module that follows these ideas is given in the example below.
| A tiny module |
|---|
|
A tiny module that has a clear separation of public interface and implementation, where the public interface is the first thing in the file and easy to read.
|
|
| Source:
show/hide
—
visit
|
/** This is an encapsulated module. **/
##push ^^
/** === Public interface === **/
/** [hypot x y] gives the length of the hypothenuse of a right-angled triangle with
** catheti x and y.
**/
hypot: -
/** [hypot3D x y z] is the 3D analog of hypot.
**/
hypot3D: hypot3D_impl
/** === End of public interface === **/
/** === Implementation === **/
##push -
hypot: \ x y → [Numeric..Math..sqrt x * x + y * y]
hypot3D_impl: \ x y z → [Numeric..Math..sqrt x * x + y * y + z * z]
##pop -
##pop ^^
|
Here the different scanner tokens that directly define values are described.
A float begins with an optional tilde sign which, when present, indicates that the number is negative. Then follows one or more decimal digits, an optional decimal point, and an optional sequence of decimal digits. An optional base 10 exponent can then be appended, prefixed with the sequence *^, negative exponents indicated using the tilde sign.
Angles are also of type
§Float, and angular units may be used as scaling factors relative to radians, which is the elementary unit of angle assumed by all trigonometric functions. The following angular units are provided by the system:
° (degrees),
deg (degrees),
rad (radians), and
grad (gradians).
Examples are given below.
| Token | Valid float? |
| 13 | Yes (= 13) |
| ~13 | Yes (= -13) |
| 2. | Yes (= 2.0) |
| ~3.14 | Yes (= -3.14) |
| ~180° | Yes (= -3.14159...) |
| 5*^~3° | Yes, (= 0.005*π/180) |
| 90deg | Yes, (= 0.5*π) |
| .609 | No (missing integer part) |
| -3.1 | No (binary minus sign) |
| 1 000 | No (spaces are not allowed) |
| 180 ° | No (space is not allowed) |
A new angular unit is defined using the following syntax, which must appear
at the beginning of a line:
##unit new_unit = float
Here,
new_unit has to be a simple identifier. The predefined unit
° is the only unit which is not a simple identifier.
A unit for an entire turn is taken as an example. The new unit will be called
turns:
##unit turns = 360°
Many users complain that they cannot type the degree character, but this useful character has been present on all keyboard layouts that I (Henrik) has encountered. To you Emacs users, note that you must type ctrl-q (that is, pressing the q key while holding down the control key), before you can use the meta key as a modifier. The following table gives a few examples of where the degree character can be found:
| OS | Keyboard layout | Key sequence | | any | Emacs | C-x 8 o | | Mac OS X | U.S. | alt-shift-8 | | Cent OS | U.S. | alt-0 | | Mac OS X | Swedish — Pro | shift-§ | | Mac OS X | Tiddish (see below) | shift-(keycode 10) |
Note that, on the Mac OS U.S. layout, the key sequence alt-0 yields the masculine ordinal indicator (º) which looks very similar to the degree sign (°) — don't confuse the two!
The Tiddish layout is my own keyboard layout, giving at the same time convenient access to Swedish characters on a Swedish keyboard, convenient access to frequent characters used in programming, and big set of logically organized dead key sequences for access to accented characters and more. The key with keycode 10 is the one with § written on it on my (Swedish) keyboard.
|
An alternative way to create negative numbers is to use the unary negation expression, for example: (-3.1). However, note that the parentheses are mandatory, thus reducing readability compared to the tilde sign alternative.
Length tokens are formed by a float (not ending with the degree sign) followed by the name of a length. New lengths can be defined as multiples of existing ones, as long as all definitions agree. Length definitions are evaluated by the program scanner, which makes them very efficient in use. The effect of a length unit defined as a more complicated expression in existing lengths, say one centimeter plus one inch, must be simulated by storing the length in a variable, which is then multiplied with a float to denote a length in this new unit.
The following lengths are provided by the system: mm, cm, m, bp (big point, also called PostScript point), and in.
| Token | Valid length? |
| 2.5cm | Yes |
| 2.5pt | No (unless the unit pt is defined) |
| ~3mm | Yes |
| 3 mm | No (space not allowed) |
| 3*^~3m | Yes (3 mm) |
| 180°mm | No (degree sign not allowed) |
A new unit of length is defined using the same syntax as for new units of angle:
##unit new_unit = length
The point used by
TeX is taken as an example. The new unit will be called
tex:
##unit tex = 0.996264009963bp
Special units of lengths are used when constructing smooth paths. Then, it is often desirable not to have to provide the distance to control points in terms of absolute distances, but one would rather specify the distance relative to the distance between the first and final interpolation point, and the angles from the first and final interpolation points to the intermediate control points.
Special lengths can be viewed as a function taken from a particular (parameterized) set of functions. There are only eight special units of lengths, and currently, there is no support for defining new ones. Here is the list of them all:
| Name | Distance | No inflexion | Circelish | Correction |
| %[D0] | √ | | | |
| %[C1] | √ | | √ | |
| %[M2] | √ | | | √ |
| %[F3] | √ | | √ | √ |
| %[d4] | √ | √ | | |
| %[c5] | √ | √ | √ | |
| %[m6] | √ | √ | | √ |
| %[f7] | √ | √ | √ | √ |
| %[i9] | | √ | | |
The meaning of the columns is the following. If there is a check mark in the Distance column, then the distance between the first and last interpolation point is used as a base length. If there is a check mark in the Circelish column, then the base length is multiplied by a factor based on the near angle, in such a way that circles are approximated well. If there is a check mark under Correction, a correction factor is applied based on the difference between the near angle and the far angle; if both angles are the same, there is no correction. If there is a check mark in the No inflexion column, then the distance to the intermediate control point is truncated to avoid inflexions, if necessary. The unit which is not based on the distance between the first and last interpolation point is based on the inflexion limit instead.
|
I know that the description of the special lengths is really bad. I hope it will be better once I start documenting path construction in general.
|
For instance, the following approximates a quarter of a circle well:
•page << [stroke (0cm,1cm)>(1%C^0°)--(1%C^90°)<(1cm,0cm)]
That is, in the first form, any single character may follow
'\" in the source code, and will become a
§Character value. No whitespace is required before the next token. The second form allows a
§Character to be created based on its Unicode code point, given in hexadecimal representation. This is more efficient than calling
..Shapes..String..Unicode, although the function offers a more flexible solution.
The third form allows a
§Character to be created based on the name of the corresponding glyph's name. No white space is allowed around the
identifier, and the identifier must be one of the names in the
Adobe GlyphList.
| Token | Valid character? |
| '"ä | Yes |
| '&U+00E4; | Yes, same as '"ä |
| '&G+adieresis; | Yes, same as '"ä |
| '&U00E4; | No (missing the mandatory +) |
| '&U 00E4; | No (space not allowed) |
| '&G+aDieresis; | No (the D should be lower case) |
The
§String construction syntax in Shapes gives three alternatives. Frist, there is a pretty one (called
normal string), with one-character pairwise delimiters that nest, then, there is the ASCII-fallback with two-character delimiters that do not nest (called
poor man's string), and finally there is one for arbitrary data (called
data string).
The reason why is has to be so complicated is that the normal string is optimized to allow TeX strings to be entered as plain as possible, which rules out any reasonable choice of escape character. Hence, the normal string cannot contain arbitrary strings of characters (since at least the terminating sequence would have to be escapable). Note, though, that the poor man's string can contain any single Unicode character. Hence, in theory, there is a way to at least enter any Unicode string as a string concatenation of individual characters, but clearly this is not an acceptable solution, and why there are data strings as well.
The
normal-string is delimited by the grave and acute accent, respectively (
`…
´). Each delimiter can be extended to include a line break on the inside. Other line breaks are part of the string literal. The delimiting accents nest (no optional line breaks this time). It is recommended that strings are entered in one of two ways among all ways to deal with line breaks. The first alternative is to enter line breaks literally and using the optional line breaks at the delimiters. The other alternative, of course, is to skip the line breaks at the delimiters and use string concatenation to insert line breaks inside the string (the data strings provide a compact way of constructing the line break). See the following examples:
| Token | Valid string? |
| `Hi there´ | Yes |
| `Shapes string: `Hi there´´ | Yes |
| `Quasiquotation: `(0 1 ,(1+1))´ | No (Unbalanced delimiter) |
| `Here's a formula: $(1+x)^{2}$´ | Yes |
`
Dear Shaper,
Multi-line...
´
| Yes (contains just one line break) |
`Dear Shaper,
Multi-line...´
| Yes, but not recommended |
|
The situation when normal strings fail (unmatched accents) is, albeit uncommon, present in standard use of TeX. Recall that the left double quote is entered as `` in TeX, but matched by ''. To deal with this, one may either resort to the poor man's string when the situation occurs, or replace the ugly two-character sequences by their proper Unicode representations instead. It is recommended to stick with normal strings, to avoid the bulkiness of the poor man's strings.
|
The syntax of a
poor-mans-string differs in two ways from normal strings. First, they are delimited using
"(\"" and
"\")". Second, the delimiters no not nest (but they have the same optional line break on the inside). Except that the delimiters are a bit bulky, this provides a very powerful way to enter most Unicode strings. There is still a technical need to be able to enter
any Unicode string, and it is a bit inconvenient to have to enter line breaks literally.
| Token | Valid string? |
| ("´") | Yes (cannot be entered conveniently using normal or data strings) |
|
The bulkiness of the poor man's string delimiters is not only a burden; it is also what makes the syntax so powerful. The only Unicode sequence it cannot handle is "), which gives an advantage over the normal string, where the acute accent can be entered only if it is preceded by a matching grave accent. However, because of the bulkiness, it is recommended to use the poor man's string only if it is required due to the presence of unmatched accents, or because the user don't know how to type the accent characters.
|
The syntax for
data-string is made up of sections, alternating between
plain and
escape mode, starting in
escape mode. The whole string begins with the sequence
"\"{". In
escape mode, pairs in the form
[A-F0-9]{2} is a base-16 representation of one unsigned byte, the range
[a-z] is reserved for named characters (currently,
n is the newline character, and
t is the tab), the characters
[ \t\n] are ignored,
"}" terminates the string,
"{" switches to
plain mode, and no other characters are allowed. In
plain mode, any character in the range
[ -z] represents itself, the
[\n] is ignored,
"}" switches back to
escape mode, and no other characters are allowed.
|
With the data strings, it is possible to enter strings that are not valid utf-8 data. It is permitted to put such data in strings, but note that they are not valid input to most functions accepting string arguments. Since arbitrary data cannot be handled as a null-terminated sequence of bytes, Shapes uses both a trailing null byte and a separate byte count.
|
Here are some examples:
| Token | Valid string? |
| "{{Hi there!}} | Yes |
| "{{The tilde (}7E{) cannot be written in plain mode.}} | Yes |
| "{7EAE00FF} | Yes (four bytes) |
| "{A0} | Yes (the newline character) |
| "{n} | Yes (same as "{A0}) |
"{
7EAE 00FF
8E7E ABCD
} | Yes (eight bytes) |
| "{1234 ABC} | No (the C needs another hex digit) |
| "{7e} | No (the e should be upper case) |
| "{7E{plain text{7E}}} | No (should be "{7E{plain text}7E}) |
"{{No trailing newline.
}} | Yes (line break is ignored) |
The valid Booleans are listed below.
| Token | Valid Boolean? |
| false | Yes |
| true | Yes |
Integers are entered with radix 10, 16, or 2, and begin with an apostrophe. The tilde sign is placed after the apostrophe for negative values, and is only allowed with radix 10. Examples:
| Token | Valid Integer? |
| '13 | Yes (= 13) |
| '~5 | Yes (= -5) |
| '0xFF | Yes (= 255) |
| '0b110 | Yes (= 6) |
| '~0xFF | No (negative integers must be entered with radix 10) |
| (-'0xFF) | Yes, but this is an expression, not a token. |
Although identifiers by themselves do not denote values, they are introduced here since they are needed in the definition of symbols below.
An identifier is made up by one or more of the characters a-z, A-Z, 0-9, the underscore, and the question mark. However, it must not begin with a number, and if it begins by the underscore, the second character must not be a number.
| Token | Valid identifier? |
| cool? | Yes |
| A_1_2 | Yes |
| __cplusplus | Yes |
| π | Yes |
| 3cm | No (this begins with a digit and is a length) |
| 2π | No (this begins with a digit and isn't even a length) |
| _3abc | No (digit after underscore in first position) |
Note that state references are not expressions:
The syntax
dyn-state is currently not used, but reserved for future use, but it is likely that it will never be used.
Users who would prefer to use the
• (bullet) over the
# (number sign) may consult the following table.
| OS | Keyboard layout | Key sequence |
| any | Emacs with shapes-mode | C-x 8 # |
| Mac OS X | U.S. | alt-8 |
| Mac OS X | Swedish — Pro | alt-q |
| Mac OS X | Tiddish (described here) | alt-(keycode 10) |
Regarding the Tiddish keyboard layout, the key with keycode 10 is the one with
§ written on it on my (Swedish) keyboard.
Note that there must not be any whitespace after the apostrophe.
Symbols are entered as the apostrophe followed by an identifier:
| Token | Valid symbol? |
| 'foo | Yes |
| '2dup | No (2dup is not an identifier) |
| '28 | No, this is an integer |
This expression obtains its meaning when a container evaluates a
§Span value. The expression should therefore not be used anywhere but in the arguments to the
..Shapes..Data..span function.
Fields and mutators have in common that they use a dot-syntax, similar to many other languages.
Any type of value in Shapes may have
fields which are referenced using identifiers. For instance, any value of type
§Coords has a field called x:
p: (1cm,2cm)
•stdout << p.x
Sometimes, a field holds a function which is parametrized by the value owning the field. Often, such fields are referred to as methods, although they are not fundamentally different from other fields. Note though, that the difference between methods and mutators is huge, see below.
Since there is no such thing as expressions referencing some kind of mutator values in Shapes, we postpone the discussion of mutators until we are ready to discuss
mutator calls, see
mutator-call.
This section describes syntax that denotes value construction in terms of other values and expressions, whithout doing so via a usual function call. Values that are constructed by calling a library function are described elsewhere. As an exception, class construction is not defined here either.
Float pairs and triples are useful generalizations of directions in 2d and 3d, and may serve other purposes as well. The way they generalize directions is that they can be multiplied by a length to yield coordinates. The drawback of using these objects to represent directions, of course, is that the origin is a valid value, but does not represent a direction. However, it is believed that the inconvenience of having to keep apart diractions and pairs/triples whould overshadow the conceptual and type safety winnings. (Internal computations, however, do keep directions and pairs/triples apart.)
The syntax for constructing pairs and triples is to separate the floats by commas, and enclose it all in parentheses. The following table gives a few examples.
| Expression | Valid construct? |
| ( 5, 7 ) | Yes, yields a float pair |
| ( 1.2, 3.4, 5 ) | Yes, yields a float triple |
| ( 5, '7 ) | No, '7 is an integer |
Sometimes, the context defines an alternative base point than can define the meaning of coordinates. To make a difference between coordinates that are relative the usual origin and the context-defined base point, the former coordinates are referred to as
offsets, constructed using the unary plus operator:
In this context, 2d and 3d refer to the perceivable space (3d) and plane (2d). Coordinates are never explicitly associated with a base frame, which would imply that coordinates denoted a particular point in the perceivable spaces. Rather, coordinates are always relative, possibly with the exception of when graphics are laid out on the output plane. However, even when graphics are placed on the output plane, they remain relative to an artificial origin, and this is particularly obvious when the output's media box is determined after the contents of the output has been laid out.
That said, we can drop the distinction of the two types of coordinates, and it is, for example, always permissible to add coordinates. The basic way to construct coordinates is similar to how pairs/triples are constructed, but with lengths instead of floats. One notable exception to this rule is that if one of the lengths in 2d are zero, it may be given as the float zero. Coordinates may also be constructed as relative an undetermined base frame, please refer to the documentation on path construction for how the base frame may be determined later.
The unary plus may be used either to construct offsets on a per-dimension level, or on a complete coordinates expression.
The following table below lists the valid constructs.
Some examples are given in the table below.
| Expression | Valid construct? |
| ( 5cm, 7in ) | Yes, yields coordinates in the perceivable plane |
| ( 5cm, 0 ) | Yes, same as ( 5cm, 0m ) |
| ( 0, 7bp ) | Yes, same as ( 0m, 7bp ) |
| ( 2mm, 7mm, 5mm ) | Yes, yields coordinates in the perceivable space |
| ( 2mm, 0, 5mm ) | No, the float zero is only allowed in 2d |
| ( (+0mm), 1mm )) | Yes, the x component is relative an undetermined base frame |
| (+ 3mm*[dir 20°]) | Yes, same as ( (+ (3mm*[dir 20°]).x), (+ (3mm*[dir 20°]).y) ) |
| ( (+0mm), 1mm, (+7mm) ) | Yes, relative coordinates may be used in both 2d and 3d |
| (+ ( 1cm, 1mm )) | Yes, but this is application of unary +, yielding the same as ( (+1cm), (+1mm) )) |
Polar handles is a special way to specify intermediate spline interpolation points. Basically, one specifies and angle and a distance instead of rectangular coordinates, but the concept is much more powerful than simply providing a convenient syntax for something like
(+ dist*[dir ang])
The power comes from the option to leave out either or both of the distance and angle. How the
free components of a polar handle are deduced is discussed under
path construction. Here, we just show the syntax for the handles themselves:
When the distance is missing, it may fall back on , so be prepared to have a binding for in dynamic scope unless you really know that it won't be needed.
|
A polar handle will store the distance part as a thunk, thereby capturing the current lexical and dynamic environments. Hence, it is not when the polar handles are used to build paths, that may be required, but when the polar handles themselves are constructed.
|
| Expression | Valid construct? |
| ( 5cm ^ 60° ) | Yes, equivalent to (+ 5cm*[dir 60°]) |
| ( 1%C ^ 60° ) | Yes, but cannot be rewritten as above |
| ( ^ 0.5 ) | Yes, angle in radians, may require a binding for |
| ( ^ ) | Yes, may require a binding for |
| ( 1%C ^ ) | Yes |
| ( 1 ^ ) | No, 1 is not a length |
| ( ^ 1cm ) | No, 1cm is not a float |
A
corner point is a generalization of
§Coord2D. The difference only matters when the point is the central point in a path point. When either or both angles to the handles of the path point are not explicitly determined, a
§Coord2D at the center causes the handles to have opposite angles. A corner point may override this by specifying another angle. The syntax is:
When the angle is not present, each angle is determined as if there was just one handle, that is, independently of the other angle.
| Expression | Valid construct? |
| ( 5cm, 4cm ^ 60° ) | Yes, corner point with 60° angle (unless both handles have specified angles). |
| ( 5cm, 4cm ^ ) | Yes, corner point with two independent handles. |
| Example |
|---|
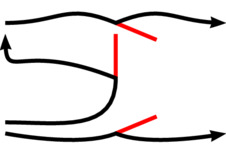 |
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
##lookin ..Shapes..Graphics
{
pth: Geometry..@defaultunit:5mm | (0cm,0cm)>(^)--(^)<(1cm,0cm^45°)>(^)--(^)<(2cm,0cm)
sl: [pth 1]
IO..•page << Traits..@stroking:Traits..RGB..RED | [Graphics..stroke sl.p--(+ ~4mm*sl.rT)]
<< [Graphics..stroke pth head:Graphics..ShapesArrow]
}
{
pth: Geometry..@defaultunit:1%C | (0cm,~1cm)>(^)--(^)<(1cm,~1cm^~45°)>(^)--(^)<(2cm,~1cm)
sl: [pth 1]
IO..•page << Traits..@stroking:Traits..RGB..RED | [Graphics..stroke sl.p--(+ ~4mm*sl.rT)]
<< [Graphics..stroke pth head:Graphics..ShapesArrow]
}
{
pth: Geometry..@defaultunit:1%F | (0cm,~9mm)>(5mm^0°)--(5mm^~90°)<(1cm,~0.5cm ^ )>(10mm^)--(5mm^~90°)<(0cm,~1mm)
sl: [pth 1]
IO..•page << Traits..@stroking:Traits..RGB..RED | [Graphics..stroke sl.p--(+ ~4mm*sl.rT)]
<< [Graphics..stroke pth head:Graphics..ShapesArrow]
}
|
The concepts of polar handles and corner points in 2d have not yet been generalized to 3d.
Functions are at the heart of a functional language. Powerful ways of creating functions make source code both more compact and more comprehensible. The language is
not curried, but contains many constructs to support
evaluated cuts, but these are presented in connection with
function calls.
There are true (pure) functions and non-pure functions, both of which are constructed similarly, but differ in how they are applied. First, pure functions will be discussed in detail. Then, non-pure functions will be presented in terms of how they differ from pure functions.
Let us begin with a very simple example, the hypothenuse function (never mind that there is dedicated syntax for this in the language already):
\ x y → [sqrt x*x + y*y]
A function with a sink can take any number of arguments, and arguments by any name. Everything that does not match the list of formals before the sink is placed in the sink, which is a
structure.
Users who would prefer to use the
→ (right arrow) over the
"->" (minus sign followed by greater-than) may consult the following table.
| OS | Keyboard layout | Key sequence |
| any | Emacs with shapes-mode | C-x 8 <right> |
| Mac OS X | Tiddish (described here) | alt-(keycode 42) shift-(keycode 50) |
Regarding the Tiddish keyboard layout, the key with keycode 42 is the one with
' (apostrophe) written on it on my (Swedish) keyboard, and the key with keycode 50 is labeled
< (less than).
Structures allows values to be grouped into a composite value, from which the components can later be extracted. The mechanism for this is designed to remind as much as possible of how multiple values are passed to a function during a function call. This creates some useful analogies. Please refer to
function application for an explanation of
named-expr, and to see how structures may be used.
Note that the type of a structure is a complex type, which we don't bother to write out here.
Besides getting parts out of a structure by applying a function to it, it is possible to bind to multiple values in the structure at once. The syntax is
The semantics reminds of a function call, but there are differences. Most importantly, the created bindings populate the
current environment, rather than a new one. The first (or only) identifier in the
split-item is the identifier for the created binding. There are ordered as well as named items; ordered items match ordered components in the structure, while named items match named components in the structure. The ordered items are those with just one identifier. When there are two identifiers, the latter is the name to be sought in the structure. When there is a quotation mark (
") instead of a second identifier, this means that the first identifier shall be used also as a second identifier.
Unlike a function application, ordered and named items do not interact; a named item cannot get its value from an ordered component in the structure. As an example, this confusing code is not legal:
s: (> '9 <)
(< foo:bar >) : s
inspite the fact that the following
is legal:
{
s: (> '9 <)
f: \ bar → { foo:bar foo }
f [] <> s
}
Named parts can also be accessed by an ordinary field reference, like this:
s: (> a:'1 b:'2 <)
•stdout << s.b
| Example |
|---|
|
| Source:
show/hide
—
visit
|
/** This feature example is named after the reminding concept from Scheme.
** Anyway, "values" refers to the possibility of returning multiple values from a function. However,
** this is not done the way it is in Scheme, where a bunch of values can only be returned through
** certain continuations. Here, multiple values are combined in one value which we denote a "structure"
** (which can be given a composite type) and special constructs are used to use a structure in function calls or to
** bind the contained values to variables.
**/
##lookin ..Shapes
/** In the first example, some values are simply put in a certain order.
**/
{
multi: \ x → (> x x+1 x+2 <)
user: \ a1 a2 a3 → 100*a1 + 10*a2 + a3
/** Note the special syntax used to call a function with the values expanded:
**/
IO..•stdout << user [] <>[multi 5] << "{n}
}
/** In the next example, some values are simply put in a certain order, and we combine this
** with an evaluated cut.
**/
{
multi: \ x → (> x a3:x+1 a2:x+2 <)
user: \ a1 a2 a3 a4 → 1000*a4 + 100*a1 + 10*a2 + a3
IO..•stdout << user [...] <>[multi 5] [] 9<< "{n}
}
/** Here, we show how to also pass states to a function, and also that the structure with values need
** not be returned from a function, but can be created anywhere. Also, it is shown how named parts
** can be accessed using field access notation.
**/
{
bunch: (> 6 a3:7 a2:8 <)
user: \ •dst a1 a2 a3 →
{
•dst << 100*a1 + 10*a2 + a3 << "{n}
}
[(user [...] <>bunch) IO..•stdout ]
/** The following syntax might be supported in the future. For now,
** it is considered a risk of ambiguity to mix the two forms of
** function application.
**/
|** [user IO..•stdout <>bunch]
IO..•stdout << `Field access: a2 = ´ << bunch.a2 << "{n}
/** By the way, parts that are not named cannot be accessed in a similar way. However,
** note that we can always to this:
**/
IO..•stdout << `The first argument is: a1 = ´ << ( \ a1 a2 a3 → a1 ) [] <>bunch << "{n}
/** ... but note that this requires that we know the names of the named parts of <bunch>, for
** otherwise there will be an error when the function is applied.
**/
}
/** Like in (lambda args <body>) construct in Scheme, we can define a function that gets just a structure as argument.
** There's also a construct that corresponds to (lambda (<arglist> . moreargs) <body>).
** In Shapes, the construct is called a "sink". Note that functions with a sink may be tricky from a type system point
** of view, so code that wish to be type-compilant should not use sinks.
**/
{
foo: \ •out <> args →
{
•out << `a = ´ << args.a << `, b = ´ << args.b << "{n}
}
[foo IO..•stdout b:2 a:1]
bar: \ •out a <> args →
{
•out << `a = ´ << a << `, b = ´ << args.b << `, c = ´ << args.c << "{n}
}
[bar IO..•stdout 0 c:2 b:1]
/** Sinks themselves cannot be passed as a named argument. Hence, the name of the sink can be used without
** confusion:
**/
boo: \ •out <> args →
{
•out << `args = ´ << args.args << "{n}
}
[boo IO..•stdout args:7]
}
/** Next, we turn to how parts of a structure can conveniently be given names in the local scope.
** The semantics remind a little bit of function calls, but are actually rather different.
**/
{
{
/** We begin with a structure with only ordered parts.
**/
bunch: (> 6 7 8 <)
{
/** Just like in a function call, we can receive the parts of a structure by order:
**/
(< x y z >): bunch
IO..•stdout << `x = ´ << x << `, y = ´ << y << `, z = ´ << z << "{n}
}
{
/** It is an error to not take care of all ordered parts. The following would result in an error.
**/
|** (< x y >): bunch
/** Unless we have a sink!
**/
(< x y <> rest >): bunch
(< z >): rest
IO..•stdout << `From the sink, z = ´ << z << "{n}
}
{
/** On the other hand, we can provide defaults if there are not enough ordered parts:
**/
(< x y z w:14 >): bunch
IO..•stdout << `w = ´ << w << "{n}
}
}
{
/** When it comes to named parts of a structure, there are some differences to the semantics of calling
** a function. First, it is not required that all named parts are received. This makes it possible to
** extract only the parts of a structure with are useful, and avoids cluttering the destination scope with
** variables of no use.
** Second, the variables being introduced in the current scope are generally named different from the
** names bound to the values in the structure.
**/
bunch: (> a1:6 a3:7 a2:8 <)
{
/** Here is a typical extraction of two named parts. Note that without the dot before the names
** that refer to parts of the structure, this would be the syntax that specifies a default values.
**/
(<
x:.a1
y:.a2
>): bunch
IO..•stdout << `x = ´ << x << `, y = ´ << y << "{n}
}
{
/** To receive the parts by their own names, the following syntax may be thought of (and implemented)
** as a low level syntax sugar.
**/
(< a2:." a3:." >): bunch
IO..•stdout << `a2 = ´ << a2 << `, a3 = ´ << a3 << "{n}
}
{
/** Defaults can be provided.
**/
def: 1000
(< a2:." a4:.":def >): bunch
IO..•stdout << `a2 = ´ << a2 << `, a4 = ´ << a4 << "{n}
}
}
{
/** Ordered and named parts can be used at the same time, as shown by these examples. However, it sould
** be noted that they cannot interact, so there are no fancy combinations to be explained here.
**/
bunch: (> 6 a3:7 a2:8 <)
{
(< x y:.a2 a3:." >): bunch
IO..•stdout << `x = ´ << x << `, y = ´ << y << `, a3 = ´ << a3 << "{n}
}
{
(< x y:1000 >): bunch
IO..•stdout << `x = ´ << x << `, y = ´ << y << "{n}
}
}
}
/** Let us also have a look at the <unlist> function here.
**/
{
/** To see the relevance of discussing <unlist> here, note that we may define a Scheme-like <apply>
** function like this:
**/
apply: \ fun args → ( fun [] <>[Data..unlist args] )
IO..•stdout << `Using apply to compute the sum of two values: ´ << [apply (+) [Data..list 4 5]] << "{n}
/** Let us now verify that it is the inverse of <list> in the following senses:
**/
lst: [Data..list 1 2 3]
showList: \ lst → [lst.foldl \ p e → ( p + ( String..newString << `(´ << e << `)´ ) ) `´]
IO..•stdout << [showList lst] << ` vs ´ << [showList ( Data..list [] <>[Data..unlist lst] )] << "{n}
struct: (> 'a 'b 'c <)
showStruct: \ struct → (( \ x y z → ( String..newString << `(´ << x << `)´ << `(´ << y << `)´ << `(´ << z << `)´ )) [] <>struct)
IO..•stdout << [showStruct struct] << ` vs ´ << [showStruct [Data..unlist ( Data..list [] <>struct )]] << "{n}
}
|
|
| stdout:
show/hide
|
567
9576
687
Field access: a2 = 8
The first argument is: a1 = 6
a = 2, b = 1
a = 0, b = 2, c = 1
args = 7
x = 6, y = 7, z = 8
From the sink, z = 8
w = 14
x = 6, y = 8
a2 = 8, a3 = 7
a2 = 8, a4 = 1000
x = 7, y = 8, a3 = 7
x = 7, y = 8
Using apply to compute the sum of two values: 9
(1)(2)(3) vs (1)(2)(3)
('a)('b)('c) vs ('a)('b)('c)
|
The basic syntax for applying (or
calling) functions is borrowed from the Scheme language. However, there is a predefined set of operators with fixed priorities that allow exceptions to this rule. In addition, special syntax is used when a function is applied over a structure, and there is syntactic sugar for calling functions of just one argument. A similar operation to calling a function is to define a new function by providing values for only some of the arguments — this is referred to as an
evaluated cut.
Besides ordinary functions, there are some other objects which the function calling syntax accepts. The other possible types of objects are affine transforms (which
should behave just as functions of a single geometric object), and paths (which can accept a path time or an arctime). The general form of a function application is
The syntax
arg-item and
state-item defined above can each be either
ordered (that is, not named) or
named, but there is a rule for how these may be ordered. The rule exist to avoid confusing situations; not because it is necessary to define the semantics. The rule is that ordered arguments (represented by
expr) must go before named arguments (represented by
named-expr), and ordered states (represented by
state) before named states (represented by
named-state).
|
Of the conceivable semantics that could be defined if named arguments were allowed to appear before ordered arguments were allowed, two will be ruled out here. First, one could simply ignore the order of appearance, and treat all named arguments just as if they appeared after the ordered arguments. This would obscure the actual position of ordered arguments without adding any power to the language. Second, one could add some power to the language by interpreting the position of ordered arguments in view of what unbound arguments there are, given the named and ordered arguments seen so far in a left to right scan. However, such semantics would also obscure the actual position of ordered arguments severely.
|
Arguments and states may appear in any order, since they do not interact at all.
It is not allowed to specify the same argument or state more than once by name.
Recall that the formal parameters of a function is an ordered list where each element has a name (with some exceptions). To define the semantics of a function call, it must be described how items in the application is mapped to formal parameters. Let us first consider the passing of arguments (as opposed to states). First, the ordered arguments in the application are mapped to the corresponding positions in the list of formal parameters. Then, the formal parameters which have not been specified by ordered arguments may be addressed by named arguemnts. Finally, default values are used for formal parameters which are still unassigned. It is an error if an unassigned formal parameter has no default value.
It is an error if there are too many arguments or if a named argument does not match the name of any formal parameter, unless the function has a sink.
The semantics for passing states is analogous to that of passing arguments.
The evaluation of argument expressions is typically delayed by passing a thunk instead of a value unless one of the following conditions hold:
- the argument expression is immediate
- the corresponding formal parameter requires the argument to be forced
(Most elementary functions in the kernel will require all their arguments to be forced, while user-defined functions only take thunks by default.)
If a state is passed as a state to a non-pure function, it may not be free in a non-immediate argument expression of the same call — it must be clear from the call expression that the argument expression where the state is free will be evaluated before the function is called.
Delaying the evaluation of argument expressions with free states could lead to some very strange behavior if the same state is also passed as a state argument; consider the following example:
f: \ •dst img → ( [[shift (~1cm,0cm)] (•dst)] & img & [[shift (1cm,0cm)] (•dst)] )
•tmp: newGroup
•tmp << [stroke [circle 3mm]]
•page << [f •tmp { •tmp << [[shift (0cm,1cm)] [stroke [circle 2mm]]] (•tmp) }]
Here, looking at the definition of f, you would expect that the program produce one two shifted copies of (•dst) and one copy of img. However, the accessing of img would change the result of (•dst) if the expression for img would not have been evaluated before the application of f.
On the other hand, delaying the evaluation of argument expressions with free states is exactly what one would expect in other situations. For instance,
[if false { •page << [stroke [circle 1cm]] } { •page << [stroke [rotate 45°][][rectangle (~1cm,~1cm) (1cm,1cm)]] }]
Here, one would certainly not expect both the circle and the rectangle to appear on the page.
Clearly, both problems would be avoided by implicitly making immediate any argument expression with a free state that is also passed as state. However, it is thought to add valuable clarity to programs to require that the mark for immediate evaluation is written out explicitly.
|
To apply a function to a single argument, one may use either of
Note that the
[] must be written as a single token without whitespace between the brackets. There is no corresponding sugar for passing states.
Both operators are left associative, and have equal precedence. Use the
[] when applying hard-wired curry functions:
fun: \ a → \ b → 10 * a + b
fun [] 2 [] 1
and use
≫ when applying a chain of unary functions:
•world << [cicle 1cm] >> stroke >> immerse >> [Geometry3D..rotate dir:(1,1,1) angle:15°]*[shift (2cm,0cm,0cm)]
When neither is the intention to obtain curried looks nor has the chain of functions more than one function, the choice becomes a matter of taste. Although messy, the following would still work:
•world << stroke [] [cicle 1cm] >> immerse >> [Geometry3D..rotate dir:(1,1,1) angle:15°]*[shift (2cm,0cm,0cm)]
Structures are special values that contain ordered as well as named components. Applying a function to a structure has the same semantics as if the ordered and named components were split in a basic function application. The syntax for calling a function with a structure is:
Note that the
[] and
<> must each be written as a single token without whitespace.
The syntax for the basic evaluated cut is simple:
Note that states cannot be bound in evaluated cuts, since this would store a reference to the state in a manner that does not match a functional language. Also note that, as in function application, ordered arguments must be passed before named arguments.
The semantics of the evaluated cut may not be quite as everone expects. Ordered arguments are simply mapped to the corresponding positions in the callee's list of formal parameters, and are bound without possibility to override in the evaluated cut. Named arguments, however, are not actually bound to the addressed formal parameters, but only assigns (or replaces) the default value for that parameter. Hence, named arguments in the evaluated cut are possible to override.
Note that it is a bad idea to use ordered arguments with a function whose list of formal parameters is unavailable for inspection. It is such a bad idea that it would be pointless at best to allow named arguments to bind permanentally to a formal parameter in an evaluated cut, since the use of this would be to change the positions of ordered arguments in an obscure way.
The following allows evaluated cuts to be constructed as easy as an unary function application:
Note that the
[...] must be written as a single token without whitespace.
The syntax to use a structure for an evaluated cut is
This section assumes that the reader is familiar with code-bracket.
Since mutators are not values in Shapes, they cannot be used in evaluated cuts in the same way as functions. However, there is sometimes a need to create a function which takes just one state argument, and invokes a mutator on that state when called.
For instance, suppose
newMap spawns a state that is used to build up a key-value map. New key-value pairs are inserted into the state using its mutator
insert, as in the following example:
•map: newMap
•map.[insert '1 `One´]
•map.[insert '10 `Ten´]
•map.[insert 'a `A symbol´]
map: freeze •map
We could get the same result without introducing the state
•map explicitly (recall
unnamed-state-expr),
map: ( newMap
<< >> \ •tmp → •tmp.[insert '1 `One´]
<< >> \ •tmp → •tmp.[insert '10 `Ten´]
<< >> \ •tmp → •tmp.[insert 'a `A symbol´]
)
but the amount of notation used here is just too much. To support the use of unnamed states in this situation, Shapes defines a syntactic sugar which allows the repeated “
\ •tmp → •tmp” to be removed:
Using the syntactic sugar, the code above simplifies to
map: ( newMap
<< >>.[insert '1 `One´]
<< >>.[insert '10 `Ten´]
<< >>.[insert 'a `A symbol´]
)
which is almost as compact as the first formulation. At the same time, it has the advantage that it is clear that the construct is free of side effects since it does not even mention a state. (The other two require more careful analysis to check whether the referred states are local to the construct or not.)
The code bracket is a rather complicated kind of expression. It is the home of many program elements, and its sementics is defined to avoid unnecessary nesting of scoping constructs. The root node of the syntax tree of a Shapes program is always a code bracket, although the enclosing braces are implicit in that case. The general form is
The top level semantics of the code brackets is defined by two phases. In the first phase, all items in the bracket that can be evaluated at any time and without evaluation of sub-expressions, are evaluated. This includes variable definitions whose right hand side can be delayed due to absence of free states. (Any items with free states are excluded from this phase.)
In the second phase, the remaining items are evaluated in order of appearance. The value of the last item is used as the value of the whole code bracket.
It is an error to place a pure expression (that is one which does not interact with states) anywhere but at the end of the code bracket. It is also an error to let a non-pure expression return with a value other than at the end of the code bracket. See
expressions for the details of pure and non-pure expressions.
The last form with the
lex-state is at the same time a kind of state node, and as such it is always evaluated in the second phase of the code bracket evaluation..
The semantics of the first form is simply to bind the variable to the value of expression. The expression is delayed unless the expression in the right hand side is immediate (see
laziness control) or has free states.
The semantics of the form with
lex-var is similar to that with
expr, and uses the simple identifier of the
lex-var for the introduced binding. For example:
": ..Shapes..Geometry..circle
is equivalent to
circle: ..Shapes..Geometry..circle
It is not recommended to do
": foo
or
"foo: foo
for that matter, to introduce an alias for a variable in the private namespace, which is when the form with
- should be used instead.
The semantics of the form with
- is similar to looking up the name of the introduced binding itself, but with the restriction to only consider the private namespace, see
lookup rules.
The semantics of the form with
lex-state is to freeze the state and bind to the final value of the state.
The state nodes are always evaluated in order of appearance in the code bracket (note also the special kind of variable definition involving a state).
The first form introduces a state. It requires a value of the special type
§Hot in the right hand side. Values of this type has the special ability to spawn fresh states. Note that a value of type
§Hot will always spawn identical fresh states, since being a
value it has no internal state of its own. On the other hand, it never spawns the
same state twice, so each state it spawns lives its own life.
The second form modifies the state by a sequence of operations. In each operation one of two kinds of operations may be performed. The first kind, without the
≫|">>", the right hand side value is passed to the state's special
tack on mutator. The only thing special about this mutator is that it is invoked with this syntax, while any other mutator must be invoked using
mutator-call (which are
non-pure expressions). The second kind of operation, indicated by the presence of
≫|">>", passes the state to the right hand side value (rather than the other way around). The right hand side must then be a function of just one state argument, returning
§Void. It is easy to construct a function which will invoke a method on the state using the
mutator-caller syntax, and although
mutator-caller must be enclosed in parentheses to be used as a general
expr, the parentheses may be omitted in this context.
The last form, denoted a freeze, prohibits future use of the state, and evaluates to the final value of the state. It is used as the end of a code bracket to return the accumulated value of a sequential computation.
A related concept is to
peek a state. This
should result in the same value that would be obtained if the state was frozen. However, it does not have to obey this rule. In addition, not all states allow the peek operation for efficiency reasons — peeking would involve an expensive deep copy in some cases. Other types of states may be possible to peek, but not to freeze. Also note that peeking a state may
poke it at the same time, that is, peeking may have side effects on the state, so two consecutive peeks need not result in the same value. The syntax is:
Note that a
state without surrounding parentheses is not an expression, and can only appear as part of a few constructs.
Peeking a state, as well as the tack-on and freeze operations described above, are special cases of
mutator calls. Ordinary mutator calls (that is, without dedicated syntax), are similar to calls to non-pure functions. Recall that state arguments can not be bound with curry. For the same reason, there is no such thing as a
mutator value; instead, when a mutator on a state is selected, it must be immediately applied. The syntax is simple:
Evaluation of a
mutator-call is just like an application of a non-pure function (denoted by the
identifier) stored in the state, with the state itself prepended to the list of arguments.
Note that while tack-on and peek could have been provided (although less conveniently) as ordinary mutators, the freeze operation has a side effect which ordinary mutators should not have; the freeze operation should release all resources used by the state, and any later references to the state are illegal.
The important thing to realize about mutator calls is that it would break semantics if a mutator could be accessed like a field of the state. To illustrate this, imagine that there was a mutator called peek, which we could apply like this:
•rnd: [newRandom (•time)]
rnd1: [•rnd.peek]
The problem is that this suggests that •rnd.peek is an expression, but expressions must evaluate to values — not states! The following makes it clear that breaking the fundamental semantic rules would be very confusing:
•rnd: [newRandom (•time)]
mutator: •rnd.peek
rnd1: [mutator]
rnd2: [mutator]
Here, it looks as if mutator was a reference to an ordinary function, which should result in the same value both times it is being invoked.
The correct way of writing (if there was a mutator called peek) is:
•rnd: [newRandom (•time)]
rnd1: •rnd.[peek]
rnd2: •rnd.[peek]
The presence of •rnd in each mutator call makes it clear that the state may be modified by each call. Now, it is clear that a new random number may result in each call.
Of course, the mutator in this example refers to the special syntax peek-state, so while the example above would not compile, the following would:
•rnd: [newRandom (•time)]
rnd1: (•rnd)
rnd2: (•rnd)
|
To declare a dynamic variable one needs to provide a filter and a top level value. The filter is applied to each new value the dynamic variable is bound to, and is primarily indended for type and range checks, but may also be used to transform values before they are actually bound. The filter must be a function of one argument. The top level value is the value of the dynamic variable until it is changed further down in the dynamic environment. The top level value is not passed through the filter. The evaluation of the top level value is delayed, which has some nice applications.
A dynamic variable may also be bound to a dynamic expression at the top level, and this is obtained using the second form of the declaration.
Typical dynamic variable declarations may not care about the possibility to use the filter for type and range checks, and look like this:
dynamic @tex_bbox_grow_abs identity 1bp
dynamic @tex_bbox_grow_rel identity 1.01
A simple filter could look like this:
dynamic @tex_bbox_grow_rel
\ new →
[if not [typeof new].isa[]Float
[error `Type mismatch for @tex_bbox_grow_rel: required a Float.´]
[if new ≤ 0
[error `Out of range error for @tex_bbox_grow_rel: required a positive value.´]
new]]
1.01
Dynamic states would be a language feature with subtleties. It is not part of the language at this time, but there is a dedicated syntax:
Often, the use of a state can be organized such that a
code-bracket only contains
state-item referencing a single state. For instance, the following code would create a message string by concatenating the string representation of some objects:
msg:
{
•tmp: newString
•tmp << `The provided value (´ << someVal << `) needs to be greater than 1´
freeze •tmp
}
This pattern is so common that Shapes provides a syntactic sugar for the same thing, where there is no need to introduce the state named
•tmp explicitly:
Using the sugar, the example simplifies to:
msg: ( newString << `The provided value (´ << someVal << `) needs to be greater than 1´ )
Note that the absence of a named state makes it easier to see that the expression is free of side effects.
Shapes supports both lexical and dynamic bindings. This section describe how to create such bindings, what their scopes are, and how to access the values of a binding. Note that a binding can never be changed.
A lexical binding is a variable whose definition can (easily) be found by a look at the source code. Code brackets and functions play an essential role for the semantics here.
Lexical binding is perhaps most easily understood from an implementation point of view. Whenever an expression is evaluated, the current lexical scope is defined by the (lexical) environment. The environment has its own bindings, that is, mapping from some identifiers to values, and a parent environment (with the exception of the global environment, which has no parent). When a lexical variable is evaluated, it is searched in the current environment, and if it is found, the variable evaluates to the value mapped to. If the variable is not found, the search continues in the parent environment, and so forth. If the search continues to the global environment, and fails there, it is an error; the variable is not bound. To understand this process in more detail, one must understand where in the source code new environments are set up, and how they are populated with mappings from identifiers to values.
First, functions set up a new environment for the passed arguments when they are called. The parent of the new environment is the environment that was in scope where the function was created (this is typically not the current environment where the function is called). The body of the function is then evaluated in the new environment. These rules simply ensure that the variables that were in scope were the function was created are also in scope when the body of the function is evaluated (except in case of shadowing).
A classic example of how lexical scoping works is the
addn function:
addn: \ n → \ x → x + n
inc: [addn '1]
•stdout << [inc '3]
The above program prints the integer 4. Note that n must be in scope when x + n is evaluated, even though n is not in scope where inc is invoked. What is important is that n is in scope where the function bound to inc was created.
Second, every code bracket sets up a new environment, under the current environment. The new environment is both home for bindings introduced in the code bracket, and becomes the current environment for the expressions evaluated in the code bracket. This means that the following is a valid code bracket:
{
a: '1
b: a + '1
b
}
So far, this seems similar to the semantics of let* in Scheme. However, the following code bracket is equivalent:
{
b: a + '1
a: '1
b
}
This reminds more of letrec in Scheme, but the reason it works has another explanation: laziness. The variables
b and
a are bound to thunks before the expression
b is evaluated.
It is possible to
reach out from the current lexical scope to circumvent
shadowing bindings. The syntax for this is
In theory, the semantics of this is simple; evaluate
expr in the lexical environment which is the parent of the current lexical environment. However, sometimes a deeper understanding of the language is required to see how many generations one must walk up the chain of environments to avoid a given binding. On the other hand, with this problem in mind, empty environments are never optimized away.
As an example of reach out, suppose we regret how we defined the paramter depth long time ago. Now we have to live with it since our function is part of a library with many users which we don't want to bother with the off-by-one change that would make our implementation of the function more natural. The following is not an option, since the function may be called with named arguments:
\ off_by_one_depth →
{
depth: off_by_one_depth - '1
/**
** Rest of body.
**/
}
Of course, we could use a new name for the adjusted depth, but pretend we are really keen to use the name
depth. Then we could use a reach-out:
\ depth →
{
/** Important! We deal with the off-by-one mistake here, once and for all.
**/
depth: ../depth - '1
/**
** Rest of body.
**/
}
Note that this changes the binding for depth in all of the code bracket, and hence it is a very good idea for readability to introduce the binding at the top of the code bracket.
| Example |
|---|
|
Mutually recursive function definitions and reach-outs.
|
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
a: 1
{
a: 2
{
a: 4
IO..•stdout << `a0 = ´ << a << "{n}
IO..•stdout << `a1 = ´ << ../a << "{n}
IO..•stdout << `a2 = ´ << ../../a << "{n}
IO..•stdout << `a1+a2 = ´ << ../(a+../a) << "{n}
}
}
{
odd: \ n → [if n = 0 false [even n-1]]
even: \ n → [if n = 0 true [odd n-1]]
IO..•stdout << `Is 0 odd? --> ´ << [odd 0] << "{n}
IO..•stdout << `Is 4 even? --> ´ << [even 4] << "{n}
}
|
|
| stdout:
show/hide
|
a0 = 4
a1 = 2
a2 = 1
a1+a2 = 3
Is 0 odd? --> false
Is 4 even? --> true
|
The value of a
dynamic binding is determined by the current
dynamic environment and cannot be determined by a simple lexical analysis. The dynamic environment is changed by the special construct
(Note that the vertical bar is not part of the BNF structure, but is the operator that indicates a change of dynamic scope.)
The semantics is simply that a new dynamic environment is set up under the current dynamic environment, and populated with the provided bindings. So far, except that the bindings are provided though special values instead of by using special syntax, this is how code brackets work. The difference is when it comes to functions. Calling a function does not change the dynamic environment. One can think of dynamic variables as a way of passing parameters to functions without explicitly providing them as arguments; the dynamic environment is always passed implicitly.
Dynamic bindings are constructed with the following syntax:
If a dynamic variable is bound to a
dynamic expression, this expression is re-evaluated in the current dynamic environment each time the dynamic variable is accessed. This way, one dynamic variable can be defined relative another dynamic variable. For instance:
dynamic @smallskip identity 2cm
dynamic @bigskip identity 5cm
test: \ •dst → { •dst << @bigskip << "{n} }
@bigskip : dynamic 4 * @smallskip
|
{
[test •stdout]
@smallskip:1cm | [test •stdout]
}
[test •stdout]
The program prints 8cm, followed by 4cm, and finally 5cm.
Dynamic variables are used extensively for controlling all parts of the graphics state. For instance, if
pth is a path to be stroked, the color and width of the stroke can be set as follows:
•page << @stroking:rgb_RED & @width:2cm | [stroke pth]
or, if there are several paths to be stroked with the same pen:
@stroking:rgb_RED
& @width:2cm
|
{
•page << [stroke pth1]
•page << [stroke pth2]
}
| Example |
|---|
|
Dynamic variables, dynamic expressions, and dynamic bindings.
|
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
/**
** First, let's have a look at some basic use of dynamic binding.
** If the first parameter after the name of the variable is the special <identity> function it is optimized away by the kernel.
** The second parameter after the name is the default value, and is not sent through the filter.
**/
dynamic @a identity 8
f: \ b → @a + b
IO..•stdout << [f 2] << "{n}
IO..•stdout << @a:6 | [f 2] << "{n}
IO..•stdout << [f 2] << "{n}
/**
** Note that the default value is delayed, so we can require that a dynamic variable must be bound by the user.
** This is also nice to know if the default expression would be expensive to compute but rarely used.
** Another application would be to detect whether the default value is ever used.
**
** However, the filter is evaluated immediately -- this simplifies the kernel business.
**/
dynamic @a_noDefault identity [error `Dynamic variable has no default binding.´]
IO..•stdout << @a_noDefault:9 | @a_noDefault << ` No error, see?´ << "{n}
dynamic @a_logDefault identity [Debug..log_before `The default value was used.´+"{n} ~9]
IO..•stdout << @a_logDefault << ` Check out the debug log!´ << "{n}
/**
** Next, we turn to dynamic expressions.
**/
dynamic @c identity 10
dynamic @b identity dynamic @a + 5
@a: dynamic @c * 4
& @c: 20
|
{
IO..•stdout << `@b: ´ << @b << "{n}
}
/**
** The rest of this file illustrates how to replace part of a dynamic bindings value by using the &| operator.
** The typical application of this would be to define a set of bindings for the text state, and then define a variation
** by changing just some of the parameters. However, since this example is meant to be text-oriented we use a silly
** mix of meaningless bindings instead.
**/
b0: Traits..@width:3mm & @a:20 & @b:21 & Traits..@stroking:[Traits..gray 0.5]
b1: Traits..@width:1mm & @b:11 & @c:12
/**
** Note that b0 & b1 would be illegal, since they both provide bindings for Traits..@width and @b.
**/
/**
** Combine b0 and b1 with priority to the bindings in b1:
**/
b01: Debug..locate [] b0 &| b1
b01
|
{
IO..•stdout << [Debug..sourceof b01] << ` :´ << "{n}
IO..•stdout << `@a: ´ << @a << "{n}
IO..•stdout << `@b: ´ << @b << "{n}
IO..•stdout << `@c: ´ << @c << "{n}
IO..•stdout << `Traits..@width: ´ << Traits..@width << "{n}
IO..•stdout << `Traits..@stroking: ´ << Traits..@stroking << "{n}
}
/**
** Combine b0 and b1 with priority to the bindings in b0:
**/
b10: Debug..locate [] b1 &| b0
b10
|
{
IO..•stdout << [Debug..sourceof b10] << ` :´ << "{n}
IO..•stdout << `@a: ´ << @a << "{n}
IO..•stdout << `@b: ´ << @b << "{n}
IO..•stdout << `@c: ´ << @c << "{n}
IO..•stdout << `Traits..@width: ´ << Traits..@width << "{n}
IO..•stdout << `Traits..@stroking: ´ << Traits..@stroking << "{n}
}
|
|
| stdout:
show/hide
|
10
8
10
9 No error, see?
~9 Check out the debug log!
@b: 85
b0 &| b1 :
@a: 20
@b: 11
@c: 12
Traits..@width: 0.1cm
Traits..@stroking: [gray 0.5]
b1 &| b0 :
@a: 20
@b: 21
@c: 12
Traits..@width: 0.3cm
Traits..@stroking: [gray 0.5]
|
The Shapes language was designed to be used with LaTeX for typesetting labels in the graphics.
The Shapes compiler goes to some lengths to avoid calling LaTeX too many times, but the problems this can cause is more of a tool matter than a language issue. Here, we shall just describe the laguage constructs that relate to producing labels with LaTeX.
First, there are a few directives that just transfer text to the top of the
LaTeX document where the labels are to appear:
##documentclass class-name
##classoption comma-separated-options
##preamble line-of-text
##documenttop line-of-text
##no-lmodernT1
##no-utf8
The default document class is
article, but this can be changed with the first of these directives. The following three directives are self-explanatory, and may appear several times. The last two disable the use of packages that are otherwise included by default. When they are not disabled, the following goes before the lines from
##preamble:
\usepackage{lmodern}
\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}
To produce the labels themselves, one simply calls the function
..Shapes..Graphics..TeX, as the following example shows.
| Example |
|---|
 |
|
| Source:
show/hide
—
visit
|
##preamble \usepackage{amsmath}
##preamble \usepackage{fancybox}
##lookin ..Shapes
IO..•page << [Graphics..TeX `
\fbox{\begin{Beqnarray*}
&\begin{aligned}
x &= 1 \\
y &= 2 % This is a comment!
\end{aligned}
\end{Beqnarray*}}
´]
|
Shapes is currently implemented using full-scale continuations, but their use is restricted by only allowing them to be bound dynamically. This restriction is enforced using special syntax to handle continuations. Note that a dynamically bound continuation merely provides the same functionality as an escape continuation.
It must be admitted that there are several features in Shapes that are not orthogonal to the use of continuations. The list below mentions the known problems briefly, but only the first item in the list concerns escape continuations.
- Delayed evaluation. Delaying the invocation of a continuation may cause unexpected results. For instance, evaluation may proceed and modify states which were not meant to be modified, or invocation of another continuation may cause the first continuation to never be invoked.
- Expression states. (This is not a problem for escape continuations.) A continuation will not capture the current state of expression states. While quite natural from one point of view (imagine capturing and restoring the state of , for instance!), this will require that the expression states are kept alive as long as an expression may be re-entered, basically breaking the local (in syntax and time) nature of expression states.
- Code bracket bindings. (This is not a problem for escape continuations.) The semantics of variable bindings in the code-bracket are similar to the letrec construct in Scheme — both hide imperative assignments, meant to be executed exactly once. As with expression states, the state of variable bindings are not captured and restored by the continuation, and it will be an error if re-entering an expression causes a variable to be bound more than once.
Dealing with these problems comes down to being cautious and careful use of forced evaluation (see
immediate-expr). Despite these warnings, the escape continuations are well suited for error handling, and their use is recommended for this purpose.
The reader is referred to the WWW for details on continuations and continuation passing style evaluation. One place to start would be the documentation for call-with-current-continuation found in
R5RS. Here, we only describe the related syntax briefely.
The construct
with-escape-continuation introduces an escape continuation in the dynamic environment (although the identifier does not look like a dynamic variable), and evaluates the expression in the new dynamic environment.
To escape through an escsape continuation, the construct
invoke-escape-continuation is used. The identifier must refer to an escape continuation in dynamic scope, and evaluation continues by evaluating the new expression with the appropriate continuation.
Since a continuation holds the information necessary to generate a backtrace, and backtraces are harmless for the semantics of a program, Shapes
does provide value-access to continuations disguised as backtraces. Evaluating
backtrace-escape-continuation results in a the referenced continuation, wrapped inside a
§Backtrace.
The keywords continuation and continue are reserved for future use.
| Example |
|---|
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
lst: [Data..list 1 2 3 4 5 6]
IO..•stdout << 10 + [lst.foldsr (\ e p •dst → { •dst << e << ` ´ p })
20 IO..•stdout]
<< ` OK!´ << "{n}
IO..•stdout << 10 + (escape_continuation leave
[lst.foldsr (\ e p •dst → [if e = 4 (escape_continue leave e) { •dst << e << ` ´ p }])
20 IO..•stdout])
<< ` OK!´ << "{n}
|
|
| stdout:
show/hide
|
6 5 4 3 2 1 30 OK!
1 2 3 14 OK!
|
|
Unlike continuations in Scheme, the escape continuations in Shapes are not invoked as if they were functions. The most important reason for this is that this would require the continuation itself to be accessible as a value, which would make it possible to invoke the continuation also in non-escaping contexts. Another good reason not to use the function application syntax is that invoking a continuation is conceptually something very different from function application for someone who doesn't think in terms of the continuation passing transform.
However, the importance of the conceptual difference may be questioned, since one can easily define a function that invokes a particular escape continuation when called:
invoke_break: \ result → (escape_continue break result)
Now, non-escaping continuations — would they be allowed in Shapes in the future — would not require special syntax to prevent the access to continuations as values. Hence, if non-escaping continuations are allowed in Shapes in the future, it is not obvious if they would be wrapped in functions (and hence invoked using function application) or invoked with special syntax. |
Since Shapes is dynamically typed, it sometimes becomes important to query and compare types. Further, it is planned that future versions of the language shall allow for user-defined types. Read on!
To support construction of detailed and correct error messages, Shapes provides a small number of expressions which reflects information about the surrounding source code.
The first two expressions,
index-of and
depth-of, give access to information about lexical bindings in any environment, but
index-of alone is particularly useful to inform about which of the arguments to a function that caused an error.
With
reflect-variable-name it is possible to get the correct variale name to which a function is being bound. The expression simply evaluates to the left hand side of the smallest variable binding expression that
surrounds the immediate parent of the
reflect-variable-name expression itself. If the smallest surrounding binding expression is shadowing the binding expression one would like to refer to, one may introduce a new variable:
fun: \ a b c →
{
myName: VARNAME
/**
** Rest of body.
**
** May use myName instead of VARNAME to avoid situations
** where VARNAME is the name of some local variable.
**/
}
(Note that the definition of
reflect-variable-name ensures that
VARNAME evaluates to
`fun´ and not
`myName´ here.)
There are many kinds of expressions. An expression can be either non-pure or pure depending on whether it interacts with states or not. An expression may also be immediate, either because it is of a certain kind which is always immediate, or because the user has flagged it to be immediate for some reason. Expressions that are non-pure or immediate cannot or must not be delayed, and are evaluated in the second phase of code bracket evaluation. While non-purity is a property that a child can (and generally does) give to its parent in the abstract syntax tree, the immediate flag is never transferred between child and parent.
The following breaks down
expr:
This section just gives the operator precedence and associativity. It is just a polished version of the corresponding segment of the Bison parser input.
In the table below, the operators have higher precedence (binds stronger) towards the bottom, and the precedence is equal in each row. Each regexp corresponds to one operator, so the rexexps with alternatives typically give an ASCII fallback for a pretty non-ASCII character. The table may contain unused operators.
| Associativity | Operators |
| non | : |
| left | ≪|"<<" |
| non | !! |
| non | →|"->" |
| right | "|" |
| left | "[]" "[!]" "[...]" "[!...]" ≫|">>" |
| right | ; |
| left | "&|" |
| left | & |
| non | : (dynamic variable binding) |
| left | ⋁|"or" |
| non | ⊻|"xor" |
| left | ⋀|"and" |
| left | ¬|"not" |
| non | = ≠|"/=" ≤|"<=" ≥|">=" |
| left | "++" -- |
| left | < > |
| left | "+" - |
| non | ∠|"/_" |
| left | "*" / ∥|"*/" |
| left | ~ |
| left | ⊙|"()" |
| left | "." |
| left | # |
| left | <> |
| left | @@ "../" |
| left | , |
The higher precedence of
: is additionally used in for the rule
where it appears as part of
named-expr.
The precedence and associativity of < and > is non-standard, but is necessary to allow for convenient path construction.
In the end, all paths are piecewise cubic splines. Parameterizing the splines as Bezier splines, we refer to interpolation points instead of spline coefficients. In general, the spline has two endpoints, and two intermediate interpolation points. The two end points may be referred to as the first endpoint and second endpoint, respectively. The intermediate interpolation points may be referred to as the first intermediate and second intermediate interpolation point, respectively. The intermediate interpolation points may be omitted as a shorthand for placing them at the neighboring endpoint.
The Bezier spline will pass through the enpoints, and be contained in the convex hull of all four interpolation points. Adjacent splines share one of the endpoints, so that the path becomes continuous. This makes it convenient to think of the path, not as a sequence of Bezier splines, but as a sequence of points on the path, where each point on the path may have a forward and a backward control point (or
handle). Please refer to the WWW for more details on the splines, for instance
Wikipedia. Here, we shall focus on how the handles may be laid out.
The syntax that constructs path points with handles is:
It is illegal to put a handle on a pathpoint which already has a handle in the same direction.
Often, paths are constructed according to the pattern
path-point-2D ( -- path-point-2D )* ( -- cycle )?
but this is just a special case of the general
It is illegal to close a path that is already closed, or to extend a closed path.
What remains to be described regarding simple paths is how the free parts of polar handles are determined. When all handles have been determined, an elementary path has been obtained, but this concept is insignificant from the user's perspective. Anyway, most of the computations on paths require an elementary path, and will trigger the following compuation if needed:
Find all angles to handles that are determined explicitly.
Propagate all known angles to any free angles on the other side of a path point (taking corner angles into account).
Compute remaining angles based on the path point's position relative its neighboring path points.
Fill in details!
Compute all distances to handles that are given explicitly. Note that this requires all angles to be known.
Propagate known distances to any free distances on the other side of a path point.
Use
..Shapes..Geometry..@defaultunit to find one value per remaining free distance. At path points where only one such value is computed, use it as it is. At path points where two such values are computed, use the smalles of these values on both sides.
Note that the rules above means that there is a subtle difference between the following two path points:
p1: (1%C^)<(0cm,0cm)>(1%C^)
p2: @defaultunit:1%C | (^)<(0cm,0cm)>(^)
|
The difference is that p1 will generally get handles of unequal length, while p2 gets handles of equal length.
|
| Example |
|---|
 |
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
##lookin ..Shapes..Geometry
h: 2cm |** This is half the height of our path
w: 1cm |** This is the width of our path
r: 4mm |** This is a corner radius
/**
** Construct a path as follows:
** Start at (0,h) and make a horizontal line to the x-coordinate (w-r). Make an (approximately) circular arc
** to the point located r to the right and r down. Make a vertical line to the y-coordinate (~h+r). Finally,
** make a smooth spline without inflexion that ends horizontally at (0,~h).
**
** Then stroke the path joined with its reverse mirrored in the y-axis.
**/
pth: @defaultunit:1%c | (0,h)--(w-r,(+0m))>(^)--(^)<(+(r,~r))--((+0m),~h+r)>(^)--(^0°)<(0,~h)
IO..•page << [Graphics..stroke pth--[[scale x:~1] [reverse pth]]]
/**
** Allow for some space around the path we want to see!
**/
IO..•page << [Graphics..stroke [rectangle (~1.5*w,~1.5*h) (1.5*w,1.5*h)]]
|
When it comes to filling paths with color, it becomes necessary to handle collections of simple paths. Sometimes, composite paths may also serve merely as a container for simple paths. The ampersand operator is used to construct composite paths:
Paths in 3d are constructed in the same way as in 2d, although their path points cannot have polar handles.
While Shapes is designed to combine functional programming and lazy evaluation with the conveniences of expression states and escape continuations, the interplay between lazy evaluation and the latter conveniences is not always transparent. Clearly,
order of evaluation is important for expressions with free states. The evaluation of
code-bracket is defined so that expressions with free states are evaluated in order of appearance. On the contrary, expressions with free states being passed as arguments in a function application will generally be delayed, and the user needs a means to prevent this.
A more delicate issue with delayed evaluation are the expressions which affect the program flow. Some functions, such as
..Shapes..error or any function which unconditionally calls
..Shapes..error, will cause the program to stop with an error message, and it is generally not the user's intention that the evaluation of calls to such functions be delayed. The Shapes language makes no distinction between such functions and other functions, so the compiler cannot conclude automatically that evaluation is not to be delayed. Similarly, evaluation of
invoke-escape-continuation or calling function which unconditionally invokes a continuation, will cause a jump in the program flow and are rarely meant to be delayed. Again, the compiler has no clue, and in both cases the user needs a means to demand immediate evaluation.
Further, prohibiting delayed evaluation may be important for efficiency reasons, and finally immediate evaluation is required to be made explicit under some circumstances.
Delayed evaluation is prohibited by flagging an expression as immediate:
| Example |
|---|
|
Two implementations of the cond construct of Scheme as a function in Shapes.
Since ..Shapes..Data..cons delays its arguments, it can be used to group a predicate with its consequence syntactically, still allowing us to evaluate the predicate by itself. All predicate-consequence pairs (which shall be §ConsPair) are received in a sink, which is turned into a list so that a fold can be used to scan the arguments from left to right. In the first implementation, called just cond, an escape continuation is used to break the fold when a pair with true predicate is found, and if the fold completes, the next expression signals an error. Note that the fold expression has no free states, so its evaluation must be made immediate explicitly. Not making immediate evaluation explicit is an error since it is generally hard to detect that the expression is meaningful to evaluate. Forcing immediate evaluation of the following call to ..Shapes..error is not necessary since it will be forced anyway by the continuation taking the result of the code bracket. The second implementation shows that the same functionality can be achieved without the use of escape continuations, but will be less efficient when there are many cases following the first true case.
|
|
| Source:
show/hide
—
visit
|
##lookin ..Shapes
##lookin ..Shapes..Control
/** This is what the standard implementation of <cond> looks like (or at least
** it did look like this at one point). It uses forced immediate evaluation.
**/
|** cond: \ <>cases →
|** (escape_continuation return
|** {
|** ![(list []<>cases).foldr
|** \ e p → [if e.car (escape_continue return e.cdr) p]
|** void]
|** ![error `No matching cond clause.´]
|** })
IO..•stdout
<< `cond: ´
<< [cond [Data..cons 1=0 `Doesn't happen, but not evaluated anyway.´]
[Data..cons 1=0 [error 'bad `(while testing cond)´ `This should never be evaluated (false case)!´]]
[Data..cons 1=1 `This is the correct answer.´]
[Data..cons 1=1 [error 'bad `(while testing cond)´ `This should never be evaluated (after true case)!´]]
[Data..cons true `This is the default, in case no other case is true.´]]
<< "{n}
purecond: \ <>cases →
{
tmp: [(Data..list []<>cases).foldr
\ e p → [if [typeof p] = Data..Type..§Void
[if e.car e p]
p]
void]
[if [typeof tmp] = Data..Type..§Void
[error 'misc VARNAME `No matching cond clause.´]
tmp.cdr]
}
IO..•stdout
<< `purecond: ´
<< [purecond [Data..cons 1=0 `Doesn't happen, but not evaluated anyway.´]
[Data..cons 1=0 [error 'bad `(while testing purecond)´ `This should never be evaluated (false case)!´]]
[Data..cons 1=1 `This is the correct answer.´]
[Data..cons 1=1 [error 'bad `(while testing purecond)´ `This should never be evaluated (after true case)!´]]
[Data..cons true `This is the default, in case no other case is true.´]]
<< "{n}
|
|
| stdout:
show/hide
|
cond: This is the correct answer.
purecond: This is the correct answer.
|
Singly linked lists are frequently used in Shapes, as they are the fundamental container of the functional paradigm. They can be constructed using functions such as
..Shapes..Data..list,
..Shapes..Data..cons, and
..Shapes..Data..fcons. The latter, being the more efficient way of prepending an element to a list, has an infix notation.
Here are some of several ways to construct singly linked lists:
lst1: [list 1 2 3] |** Efficient construction, efficient representation.
lst2: 1 ; 2 ; 3 ; nil |** Step by step construction, efficient representation.
lst3: [cons 1 [cons 2 [cons 3 lin]]] |** Lazy construction, inefficient representation.
The expansions of
unary which have not been described elsewhere are given here. Note that the unary plus and minus signs are completely unrelated operations. The special syntax for calling the
..Shapes..Numeric..Math..abs function is also included here.
This section remains to be written. Please refer to the operator listings for any particular type.
This section remains to be written. Please refer to the operator listings for any particular type.


