3<span class="medium-caps"><sup>d</sup></span> graphics

To top. Up: User's guide index

This guide presents basic ideas and tools for 3^d graphics in Shapes. A primary design goal has been to make a tight integration of 3^d with 2^d. With the ability to define surfaces in 3^d comes a need to use light models to enhance the 3^d experience, and we will look briefly at this towards the end of the guide.

Sections: Geometry Coordinates and paths Basic drawing Stereo images Light modeling

As was said above, tight integration of 3^d with 2^d has been a main design goal. The model used is that the 2^d world is the image plane of a pin-hole camera, and coincides with the plane z = 0. When the 3^d world is projected onto the image plane of the camera, the position of the eye (that is, the pin-hole of the camera) is ( 0, 0, z_eye ), which the user can affect by binding ..Shapes..Geometry3D..@eyez, see the figure below.

Geometry of the view projection

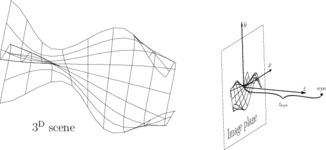
The relation between the 3^d scene and the 2^d image plane where the 3^d scene is projected by ..Shapes..Geometry3D..view. The source is not meant to be instructive.

Source: show/hide — visit
##needs ..Shapes..Data / seq-support ##needs ..Shapes..Graphics / braces ##needs ..Shapes..Graphics3D / metapostarrow ##needs ..Applications..Blockdraw ##lookin ..Shapes ##lookin ..Shapes..Geometry3D ##lookin ..Shapes..Graphics3D ##lookin ..Applications..Blockdraw dir: Geometry..dir normalized: Geometry..normalized R: 5cm u: R/2.1 / The function describing the manifold. / surfz: \ p → (0.24R) [Numeric..Math..sin (p.x/u) * (p.y/u)] / A general-purpose helper. / surfit: \ f p → ( p.x, p.y, [f p] ) / A general-purpose surface-circle. / surfaceCircle: \ f r c sides:'12 → { mid: [surfit f c] [[Data..range '0 sides-'1].foldl \ p e → p & [Graphics..fill mid--[surfit f c+r[dir (360°e)/sides]]--[surfit f c+r[dir (360°(e+'1))/sides]]--cycle] null] } foldpairsl: { helper: \ op zero last lst → [if [Data..nil? lst] zero [helper op [op zero last lst.car] lst.car lst.cdr]] \ op zero lst → [if [Data..nil? lst] lst [helper op zero lst.car lst.cdr]] } foldtriplesl: { helper: \ op zero back2 back1 lst → [if [Data..nil? lst] zero [helper op [op zero back2 back1 lst.car] back1 lst.car lst.cdr]] \ op zero lst → [if [Data..nil? lst] lst [if [Data..nil? lst.cdr] Data..nil [helper op zero lst.car lst.cdr.car lst.cdr.cdr]]] } functionMesh: \ zMap xRange yRange step:'1 → { xyz: \ p → ( p.x, p.y, [zMap p] ) [[Data..downsample xRange step].foldl \ p x → p & [Graphics..stroke [yRange.foldl \ p y → p--[xyz (x,y)] Geometry3D..emptypath ]] null] & [[Data..downsample yRange step].foldl \ p y → p & [Graphics..stroke [xRange.foldl \ p x → p--[xyz (x,y)] Geometry3D..emptypath ]] null] } functionSurface: \ zMap xRange yRange → { xyz: \ p → ( p.x, p.y, [zMap p] ) [foldpairsl \ p x1 x2 → p & [foldpairsl \ p y1 y2 → p & { p11: [xyz (x1,y1)] p12: [xyz (x1,y2)] p21: [xyz (x2,y1)] p22: [xyz (x2,y2)] pc: [xyz (0.5(x1+x2),0.5(y1+y2))] [Graphics..fill pc--p11--p12--cycle] & [Graphics..fill pc--p12--p22--cycle] & [Graphics..fill pc--p22--p21--cycle] & [Graphics..fill pc--p21--p11--cycle] } null yRange ] null xRange ] / & [functionMesh zMap xRange yRange] / } ridgeLines: { ridgeTest: \ p1 p2 o1 o2 → { d11: [normalized o1 - p1] d12: [normalized o2 - p1] dm1: d11 + d12 d21: [normalized o1 - p2] d22: [normalized o2 - p2] dm2: d21 + d22 dc: [normalized p2 - p1] ( dm1dc ≤ dm1d11 ) and ( ~(dm2dc) ≤ dm2d22 ) } \ zMap xRange yRange tf → { xyz: \ p → ( p.x, p.y, [zMap p] ) [foldpairsl \ p x1 x2 → [foldpairsl \ p y1 y2 → { p11: [xyz (x1,y1)] >> tf >> view p12: [xyz (x1,y2)] >> tf >> view p21: [xyz (x2,y1)] >> tf >> view p22: [xyz (x2,y2)] >> tf >> view pc: [xyz (0.5(x1+x2),0.5(y1+y2))] >> tf >> view pc3D: [xyz (0.5(x1+x2),0.5(y1+y2))] p & [if [ridgeTest p11 pc p12 p21] [Graphics..stroke [xyz (x1,y1)]--pc3D] null] & [if [ridgeTest p12 pc p11 p22] [Graphics..stroke [xyz (x1,y2)]--pc3D] null] & [if [ridgeTest p22 pc p12 p21] [Graphics..stroke [xyz (x2,y2)]--pc3D] null] & [if [ridgeTest p21 pc p11 p22] [Graphics..stroke [xyz (x2,y1)]--pc3D] null] } p yRange ] null xRange ] & [foldtriplesl \ p x1 x2 x3 → [foldpairsl \ p y1 y2 → { p1: [xyz (x2,y1)] >> tf >> view p2: [xyz (x2,y2)] >> tf >> view pc1: [xyz (0.5(x1+x2),0.5(y1+y2))] >> tf >> view pc2: [xyz (0.5(x2+x3),0.5(y1+y2))] >> tf >> view [if [ridgeTest p1 p2 pc1 pc2] p & [Graphics..stroke [xyz (x2,y1)]--[xyz (x2,y2)]] p] } p yRange ] null xRange ] & [foldtriplesl \ p y1 y2 y3 → [foldpairsl \ p x1 x2 → { p1: [xyz (x1,y2)] >> tf >> view p2: [xyz (x2,y2)] >> tf >> view pc1: [xyz (0.5(x1+x2),0.5(y1+y2))] >> tf >> view pc2: [xyz (0.5(x1+x2),0.5(y2+y3))] >> tf >> view [if [ridgeTest p1 p2 pc1 pc2] p & [Graphics..stroke [xyz (x1,y2)]--[xyz (x2,y2)]] p] } p xRange ] null yRange ] } } T_obj: [shift (0cm,0cm,~10cm)][Geometry3D..rotate dir:(1,0,0) angle:~90°-~19°][Geometry3D..rotate dir:(0,0,1) angle:~90°+25°] N_major: '8 N_minor: '2 xRange: [Data..range ~R R count: N_major * N_minor + '1] yRange: [Data..range ~R R count: N_major * N_minor + '1] world: ( @eyez:5cm \| { •imagePlane: Graphics..newGroup •imagePlane << Traits..@width:0.8bp \| [view T_obj [] ( newZSorter << Traits..@nonstroking:Traits..BW..OCCLUDING \| [functionSurface surfz xRange yRange] << [functionMesh surfz xRange yRange N_minor] << [ridgeLines surfz xRange yRange T_obj] ) ] •imagePlane << Traits..@width:0.3bp \| [Graphics..stroke [Geometry..rectangle (~3cm,~3cm) (3cm,3cm)]] << [Geometry..shift (~3cm,~3cm)+(5mm,5mm)] [] [Graphics..TeX `{\Huge Image plane}´] •world: newGroup len: 4cm •world << [immerse (•imagePlane)] << [Graphics..stroke (0cm,0cm,0cm)--(len,0cm,0cm) head:[MetaPostArrow ahLength:3mm normal:(0,0,1) ...]] << [Graphics..stroke (0cm,0cm,0cm)--(0cm,len,0cm) head:[MetaPostArrow ahLength:3mm normal:(0,0,1) ...]] << [Graphics..stroke (0cm,0cm,0cm)--(0cm,0cm,len) head:[MetaPostArrow ahLength:3mm normal:(1,0,0) ...]] << [shift (len,0cm,0cm)] [] [facing [putlabelAbove [Graphics..TeX `$\hat{x}$´] (0cm,0cm) 1]] << [shift (0cm,len,0cm)] [] [facing [putlabelRight [Graphics..TeX `$\hat{y}$´] (0cm,0cm) 1]] << [shift (0cm,0cm,len)] [] [facing [putlabelAbove [Graphics..TeX `$\hat{z}$´] (0cm,0cm) 1]] << [shift (0cm,0cm,@eyez)] [] [facing [Graphics..fill [Geometry..circle 2bp]]] << [shift (0cm,0cm,@eyez)] [] [facing [putlabelAbove [Graphics..TeX `eye´] (0cm,1mm) 0]] << [Graphics..Tag..tag 'eye (0cm,0cm,@eyez)] << [Graphics..Tag..tag 'origin (0cm,0cm,0cm)] bracePath: [Geometry3D..rotate dir:(0,1,0) angle:~90°] [] [immerse [Graphics..someClosedBrace (0cm,0cm) (@eyez,0cm)]] •world << [Graphics..fill bracePath] \|** Next, I use that I happen to know that the tip of the brace is at path time 1. •world << [shift [bracePath 1].p] [] [facing [putlabelBelow [Graphics..TeX `$z_{\mathrm{eye}}$´] (0m,0m) 0]] freeze •world } ) T_view: [shift (0cm,~40cm,0cm)][Geometry3D..rotate dir:(0,1,0) angle:65°][Geometry3D..rotate dir:(0,0,1) angle:15°][Geometry3D..rotate dir:(1,0,0) angle:5°] @eyez:∞ \| { theView: Traits..@width:0.3bp \| [view (T_view T_obj) [] ( newZSorter \|** << Traits..@nonstroking:Traits..BW..OCCLUDING \| [functionSurface surfz xRange yRange] << [functionMesh surfz xRange yRange N_minor] << [ridgeLines surfz xRange yRange T_view * T_obj] ) ] IO..•page << theView << [view (T_view * T_obj) [] [facing [putlabelBelow [Graphics..TeX `{\huge $3^{\mathrm{D}}$ scene}´] (~2cm,~3cm) 0]]] << [view T_view [] world] }

The projection is performed by applying the function ..Shapes..Geometry3D..view. The reverse, to take an object in the 2^d world and equip it with a z = 0 coordinate, is performed by the function ..Shapes..Geometry3D..immerse.

An alternative to ..Shapes..Geometry3D..immerse is ..Shapes..Graphics3D..facing, which is useful to position things as labels in a 3^d scene.

One very important tool for the interaction between 3^d and 2^d is the use of tags. When tags in a 3^d scene are viewed, they will be converted to 2^d tags and reference the viewed version of the tagged objects. It is particularly useful to tag points in a 3^d scene.

Coordinates in 3^d are entered according to coords-3D, for instance ( 3mm, 7mm, 1cm ).

At the time of writing, path construction in 3^d is very limited compared to 2^d, as there are no automatic choices of angles or distances to interpolation points. One can use both absolute and relative coordinates, though. An example of a path in 3^d can be found in the straight stereo projection example below.

Fortunately many of the paths used in 3^d lie in a plane, and can be constructed by creating them in 2^d first, and then immerse and transform to get it in the right position.

The functions ..Shapes..Graphics..stroke, ..Shapes..Graphics..fill, and ..Shapes..Graphics..fillstroke are applicable to paths in 3^d. The operations are defined to generate objects that, when viewed, the corresponding 2^d operations are applied to the view of the path. This means that filling and fill-stroking paths which are not contained in a plane may not be entirely wise. Surfaces that can be painted in the light model, described below, are basically limited to be flat and are not created by ..Shapes..Graphics..fill.

Arrowheads in 3^d can be tricky to get right. See ..Shapes..Graphics / arrowheads for details. Also note the approach illustrated under ..Shapes..Graphics3D..facing.

Sometimes the pin-hole view of a 3^d scene fails to give a good impression of a 3^d scene, and then it may help to draw a the image in stereo. This means that one draws one picture for each human eye, and put the images side by side so that one can see both at the same time, and this often greatly enhance the illusion of a 3^d scene if done correctly. There is no special support for drawing images in stereo in Shapes, but this section shows that there is no need for that; it is merely a question about applying the right transforms.

There are two approaches to stereo projections; to put the left eye's image to the left of the right eye's image, or vice versa. In the first case, one must look towards a point at infinity (or very far away, or beyond infinity…), and in the second case one must look towards a point between the image plane and the eyes. It is both a matter of personal comfort and taste, and technical reasons, which approach to choose. Since it is extremely difficult to look towards a point beyond infinity the first approach is limited to objects of smaller width than the distance between the eyes. This limitation is not present in the other approach, but at least for me it is very difficult to get the eyes to focus in this case (the brain thinks the object is much closer than the distance to the paper, and apparently this is more disturbing than when the brain thinks the object is at infinity even though the paper much closer than so.). The first approach is referred to as a straight stereo projection, while the other is referred to as a cross stereo projection.

To make a straight stereo projection, for the distance eyew between the eyes we shall make two projections of the scene, differing by a x shift of this length. Note that the scene is shifted to the left for the right eye, and vice versa, and hence the images have to be swapped before drawn. The following example shows this technique.

Straight stereo projection

A straight stereo projection, that is, the left eye's view to the left of the right eye's view. The simple geometry behind this is described in the text.

Source: show/hide — visit
##lookin ..Shapes ##lookin ..Shapes..Geometry3D rot: [rotate (1,1,1) 30°] screwSeg: (~1cm,1cm,~1cm)<(~1cm,0cm,~1cm)>(~1cm,~1cm,~1cm)--(1cm,~1cm,~2cm)<(1cm,0cm,~2cm)>(1cm,1cm,~2cm) deeper: \ n → [shift (0cm,0cm,n~2cm)] screw: [scale 1.5] [] (1cm,~1cm,0cm)<(1cm,0cm,0cm)>(1cm,1cm,0cm)--screwSeg--[[deeper 1] screwSeg]--[[deeper 2] screwSeg]--cycle •world: Graphics3D..newGroup •world << Traits..@width:0.3bp & Traits..@stroking:[Traits..gray 0.5] \| [Graphics..stroke screw] markStart: 0.15 markCount: '5 paintLeg: \ pth → ( [Graphics..stroke pth] & ( Traits..@nonstroking:Traits..RGB..BLACK \| [Graphics..fill [shift pth.end.p][][immerse [Geometry..circle 1.5bp]]] ) ) •world << [[Data..range '0 markCount-'1].foldl \ p i → { sl: [screw (markStart + i(1/markCount))[Numeric..Math..abs screw]] len: 2.5cm p & ( Graphics3D..newGroup << Traits..@stroking:Traits..RGB..RED \| [paintLeg sl.p--(+(lensl.T))] << Traits..@stroking:Traits..RGB..GREEN \| [paintLeg sl.p--(+(lensl.N))] << Traits..@stroking:Traits..RGB..BLUE \| [paintLeg sl.p--(+([if i = '0 ~1 1]lensl.B))] << [shift sl.p+(~2mm,3mm,0mm)] [] [Graphics3D..facing [Layout..center_x [Graphics..TeX [String..sprintf `\textbf{%d}´ i+'1]]]] ) } Graphics3D..null] •world << [shift (~1.5cm,~1.5cm,0cm)] [] [Graphics3D..facing [Layout..center_x [Graphics..TeX `Odd one out!´]]] world: freeze •world { world: [rotate (1,1,1) 30°] [] ../world eyew: 5.0cm IO..•page << view [] world IO..•page << world >> [shift (~eyew,0cm,0cm)] >> view >> [Geometry..shift (2eyew,0cm)] }

The next example shows the same application, but with a cross stereo projection.

Cross stereo projection

A cross stereo projection, that is, the left eye's view to the right of the right eye's view. The simple geometry behind this is not described in the text.

Source: show/hide — visit
##lookin ..Shapes ##lookin ..Shapes..Geometry3D rot: [rotate (1,1,1) 30°] screwSeg: (~1cm,1cm,~1cm)<(~1cm,0cm,~1cm)>(~1cm,~1cm,~1cm)--(1cm,~1cm,~2cm)<(1cm,0cm,~2cm)>(1cm,1cm,~2cm) deeper: \ n → [shift (0cm,0cm,n~2cm)] screw: [scale 1.5] [] (1cm,~1cm,0cm)<(1cm,0cm,0cm)>(1cm,1cm,0cm)--screwSeg--[[deeper 1] screwSeg]--[[deeper 2] screwSeg]--cycle •world: Graphics3D..newGroup •world << Traits..@width:0.3bp & Traits..@stroking:[Traits..gray 0.5] \| [Graphics..stroke screw] markStart: 0.15 markCount: '5 paintLeg: \ pth → ( [Graphics..stroke pth] & ( Traits..@nonstroking:Traits..RGB..BLACK \| [Graphics..fill [shift pth.end.p][][immerse [Geometry..circle 1.5bp]]] ) ) •world << [[Data..range '0 markCount-'1].foldl \ p i → { sl: [screw (markStart + i(1/markCount))[Numeric..Math..abs screw]] len: 2.5cm p & ( Graphics3D..newGroup << Traits..@stroking:Traits..RGB..RED \| [paintLeg sl.p--(+(lensl.T))] << Traits..@stroking:Traits..RGB..GREEN \| [paintLeg sl.p--(+(lensl.N))] << Traits..@stroking:Traits..RGB..BLUE \| [paintLeg sl.p--(+([if i = '0 ~1 1]lensl.B))] << [shift sl.p+(~2mm,3mm,0mm)] [] [Graphics3D..facing [Layout..center_x [Graphics..TeX [String..sprintf `\textbf{%d}´ i+'1]]]] ) } Graphics3D..null] •world << [shift (~1.5cm,~1.5cm,0cm)] [] [Graphics3D..facing [Layout..center_x [Graphics..TeX `Odd one out!´]]] world: freeze •world { eyew: 5.0cm lift: 0.5@eyez world: [scale 0.4][rotate (1,1,1) 30°] [] ../world IO..•page << world >> [shift (0.5eyew,0cm,lift)] >> view >> [Geometry..shift (~0.5eyew,0cm)] IO..•page << world >> [shift (~0.5eyew,0cm,lift)] >> view >> [Geometry..shift (0.5*eyew,0cm)] }

Surfaces whose color is affected by the light model are created using ..Shapes..Graphics3D..facet. Light sources are created using any of ambient_light, specular_light, or distant_light. When surfaces and light sources are combined in a §•ZBuf (see ..Shapes..Graphics3D..newZBuf) or a §•ZSorter (see ..Shapes..Graphics3D..newZSorter), the light computations will be executed when ..Shapes..Geometry3D..view is applied. The rest of this section will be devoted to discussing the many options that exist for these objects.

3d graphics

Geometry

Coordinates and paths

Basic drawing

Stereo images

Light modeling

3^d graphics