For version 0.7.0.
To top.  Up: ..Shapes..Graphics

[standard prelude]

shapesarrow

Alphabetical index
ShapesArrow
Namespace:  ..Shapes..Graphics
Please refer to ..Shapes..Graphics / arrowheads for an introduction to arrowheads.
ShapesArrow
p::§Path width:3::( §Length ∪ §Float ) frontAngle:40°::§Float rearAngle:150°::§Float fillAsStroking:true::§Boolean → (> picture::§Drawable cut::§Length <)
Dynamic references:none
This arrowhead does not inherit the parameterization from MetaPostArrow, although frontAngle corresponds to ahAngle. Instead of ahLength, there is width, and there is the additional parameter rearAngle.
If width is a §Float, it is implicitly multiplied by ..Shapes..Traits..@width, but truncated at 3 bp from below. Widths smaller than 3 bp can still be obtained by specifying the width directly as a §Length. By defining an arrowhead as a dynamic variable, it is even possible to make the width your own function of ..Shapes..Traits..@width, like so: 
dynamic @myHead identity dynamic [ShapesArrow width:@width*(1.5+4.5bp/(1bp+@width)) ...]
An example is included to illustrate how the shape of the arrowhead is determined.
Geometry of the ShapesArrow
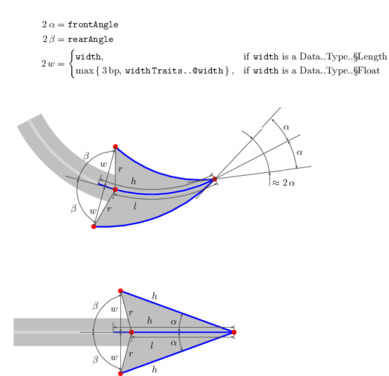Angry
The shape of the ShapesArrow arrowhead on a bent path is defined by generalization of how the arrowhead is defined for straight paths. Looking at the arrowhead on the straight path, the shape of each triangular hook is determined by the length w and the angles α and β. From the triangle, the distances r, h, and l are determined. From the red point at the rear of the arrowhead, the tangent direction at that point, the angle β, and the distance r, the outer red points are determined. The outer blue paths are then obtained by scaling and rotation of the central blue path of length h, so that they join the front red point with the corresponding outer red point. The outer red points are connected with straight lines to the rear red point.
Note that the construction of the arrowhead does not (unless the path is straight) result in an angle of exactly frontAngle at the front, and that the two tangents at the front may not be symmetric with respect to the tangent direction of the underlying path. However, as the illustration shows, the deviations may hardly be noticeable.
Source: show/hide — visit
Get Shapes at SourceForge.net. Fast, secure and Free Open Source software downloads